平衡流

在大气科学和海洋科学中，平衡流是大气与海洋运动的理想化模型。理想化之处在于考虑具有恒定密度的一个孤立流体质点的行为，它在水平面上的运动受到选定的作用力的影响，最后达到近似平衡。平衡流分析往往以大气运动作为对象，在少数情况下也可以应用到海洋流动的分析中。

平衡流通常是实际气流的准确近似值，有助于提高对大气运动的定性理解和解释。特别是，平衡流的速度可以用作对地球表面特定气压分布之下的风速的估计。

自然坐标系中的动量方程

轨迹

动量方程主要是为获取在水平面上流体质点运动的一般轨迹的方程。流体质点的位置由它在时间t所经过的轨迹s = s ( t ) 上的距离定义。然而，实际上，轨迹是作用在质点上的力平衡的结果。在本节中，为了方便表示，我们假设从一开始就知道轨迹的位置。当我们考虑由接下来选择的力所决定的运动时，我们将知道哪种类型的轨迹适合特定的力平衡。

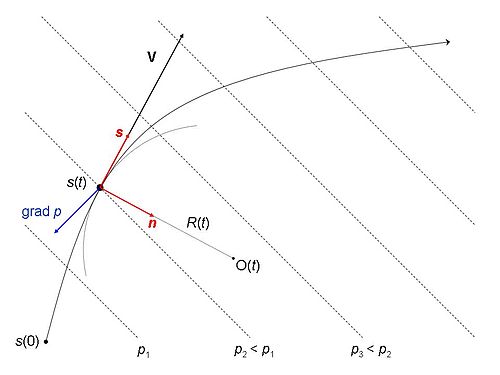
位置s处的轨迹有一个切线单位向量s ，它始终指向s'增长方向，以及一个垂直于s的单位向量n ，它指向局部曲率中心 O。曲率中心位于弯道的“内侧”，并且可以根据其形状在轨迹的任一侧移动。宗地位置与曲率中心之间的距离是该位置的曲率半径R。曲率半径在轨迹变直的点处接近无限长，并且在这种特殊情况下未确定n的正方向（在地转流中讨论）。参考系 ( s, n ) 由图中的红色箭头表示。这个框架被称为自然的或内在的，因为轴不断地适应移动的气块，因此它们与它的命运最密切相关。

运动学

速度矢量 ( V ) 的方向与s类似，并且具有速率V = d s /d t 。这个速率总是一个正数，因为任何包裹都沿着自己的轨迹移动，并且随着时间的增加（d t >0），踩踏的长度也会增加（d s >0）。

气块的加速度矢量分解为平行于s的切向加速度和沿正n的向心加速度。切向加速度仅改变速度V并且等于 D V /D t ，其中D/Dt表示物质导数。向心加速度始终指向曲率中心 O 并且仅在包裹移动时改变向前位移的方向s 。

力

在平衡流理想化中，我们考虑三向力平衡：

气压梯度力。这是由于周围大气气压p的空间差异对气块产生的作用。（时间变化不重要) 气压的空间变化通过等压线可视化，等压线是连接气压具有相同值的位置的等高线。在图中，这由等距的直线简单地表示。作用在气块上的气压减去p的梯度向量（符号为： grad p ）——在图中绘制为蓝色箭头。在所有点上，气压梯度都指向p最大增加的方向，并且始终垂直于该点的等压线。由于流动包感受到从较高气压到较低气压的推动，因此有效气压梯度力与气压梯度方向相反，因此出现梯度矢量之前的负号。
摩擦力。这是一个始终与向前运动相反的力，因此该矢量总是沿负方向s作用，从而降低速度。在平衡流模型中起作用的摩擦是由地球表面的粗糙度对上方移动的空气施加的。为简单起见，我们在这里假设摩擦力（每单位质量）通过恒定摩擦系数K成比例地调整到包裹的速度。在更现实的条件下，摩擦对速度的依赖性是非线性的，除了缓慢的层流。
科里奥利力。由于地球的自转，这一作用往往会使任何在北（南）半球行进的物体向其右（左）移动。其每单位质量的强度与速度V成正比，并且从赤道（其为零）向两极增加的幅度与当地的科里奥利频率f （赤道以北的正数和负的南部）成正比。因此，科里奥利矢量总是指向侧面，即沿n轴。它在平衡方程中的符号可能会改变，因为n的正方向仅根据其曲率在轨迹的左右翻转，而科里奥利矢量根据数据包在地球上的位置指向任一侧。科里奥利力的精确表达比科里奥利参数和气块速度的乘积要复杂一些。然而，这种近似与忽略了地球表面的曲率是一致的。

在图中绘制的虚拟情况下，气压差将气块沿轨迹向前推，并相对于弯道向内；科里奥利力将北（南）半球的弯道向内（向外）推；摩擦力（必然）向后迟滞。

主导方程

对于气块的动态平衡，加速度的任一分量乘以气块的质量等于作用在同一方向上的外力的分量。由于气块的平衡方程是用自然坐标编写的，因此单位质量水平动量的分量方程表示如下： ${\frac {DV}{Dt}}=-{\frac {1}{\rho }}{\frac {\partial p}{\partial s}}-KV$ ${\frac {V^{2}}{R}}=-{\frac {1}{\rho }}{\frac {\partial p}{\partial n}}\pm fV,$ 分别在前向和侧向方向，其中 ρ 是空气的密度。

这些项可以分解如下：

${DV}/{Dt}$ 是气块的时间变化率（切向加速度）；
$-{\partial p}/{\partial s}$ 是沿轨迹的每单位体积的气压分量；
$-KV$ 是由于摩擦引起的减速度；
${V^{2}}/{R}$ 是向心加速度；
$-{\partial p}/{\partial n}$ 是垂直于轨迹的每单位体积气压的分量；
$\pm fV$ 是每单位质量的科里奥利力（符号模糊度取决于力矢量和n的相互方向）。

稳态假设

在下面的讨论中，我们考虑稳态流动。因此，速度不能随时间变化，产生切向加速度的分力需要总和为零。换句话说，主动和阻力必须在向前的方向上平衡，以便 $DV/Dt=0$ .重要的是，还没有假设右侧的力在那里是显着的还是可以忽略不计的。此外，轨迹和流线在稳态条件下重合，并且成对的形容词切向/正常和流向/交叉流变得可以互换。切向加速度不可忽略的大气流动称为等压流动。

速度方向仍然可以沿着轨迹在空间中改变，不包括惯性流，由气压模式设定。

总体框架

模式化

省略切向和法向平衡方程中的特定项，我们得到以下五种理想化流动之一：反三向流动、地转流动、旋衡流动、惯性流动和梯度流动。对应大气科学中的五种风：逆转风、地转风、旋衡风、惯性风和梯度风。通过对剩余项的平衡进行推理，我们可以明白：

什么样的气压场分布支持这种流动；
气团沿着哪个轨迹行进；
流速多少。

以下是/否表显示了在每个理想化中考虑了哪些贡献。为了完整起见，还提到了埃克曼层的模式化，并单独处理，因为它涉及空气的内部摩擦，而不是空气和地面之间的摩擦。

	逆流	地转流	旋转流	惯性流	梯度流	埃克曼流
惯性离心力（曲率）	否	否	是	是	是	否
摩擦力	是	否	否	否	否	是
气压	是	是	是	否	是	是
科里奥利力	否	是	否	是	是	是

局限性

空气特性的垂直差异

据说这些方程适用于在水平面上移动的空气块。事实上，当人们考虑一列大气时，很少出现空气密度在整个高度上都相同的情况，因为温度和水分含量，因此密度，确实会随着高度而变化。这样一列中的每个包裹都根据其自身高度的空气属性移动。

只要较轻的空气在较重的空气顶部稳定分层会导致分层良好的空气层，均匀的空气层可能会一层一层地滑动。但是，如果某些空气恰好比周围的空气重/轻，则确实会发生垂直运动并反过来改变水平运动。在自然界中，下降气流和上升气流有时会比平行于地面的运动更迅速、更强烈。平衡流方程不包含代表下沉/浮力作用的力或速度的垂直分量。

还要考虑气压通常是通过地面/海平面附近的仪器（气压计）测得的。普通天气图的等压线汇总了这些气压测量值，并根据平均海平面调整了在某一特定时间的呈现一致性。这些数值代表了空气柱顶的重量，并不表示空气比重的变化细节。此外，根据伯努利定理，如果空气发生显著的垂直运动，测得的气压并不完全是气柱的重量。因此，通过测量值并不能真正知道作用在不同高度的单个空气块上的气压。在平衡流动公式中使用表面气压图中的信息时，最好将力视为施加于整个空气柱。

然而，在靠近地面/海洋的地方，每个气柱中总是会出现一个空气速度差异，如果任何地方的空气密度相同并且没有发生垂直运动，也是如此。在那里，接触面的粗糙度减缓了上方的空气运动，这种减速效果随着高度的增加而逐渐减弱。例如，参见行星边界层。摩擦反绊流适用于地面附近，而其他模式适用于离地面足够远的地方，不会感觉到它的“制动”效果（自由气流）。这是在概念上保持两个组分开的原因。从低引用模式到高引用模式的过渡由类似埃克曼层的模式连接，其中空气对空气的摩擦、科里奥利和气压处于平衡状态。

总之，平衡流速度很好地适用于可以被视为均匀（恒定密度，无垂直运动）或最多稳定分层（非恒定密度，但没有垂直运动）的空气柱。如果我们无法验证这些情况的发生，估计就会出现不确定性。由于摩擦力的开关处理，他们也无法描述整个气柱从与地球的接触表面到外层大气的运动。

空气特性的横向差异

即使气柱在高度上是均匀的，每个气柱的密度也会因位置而异，首先因为气团的温度和水分含量因来源而异；然后由于气团在流过地球表面时会改变它们的特性。例如，在温带气旋中，围绕低压循环的空气通常带有一个温度较高的扇区，该扇区楔入较冷的空气中。气旋循环的梯度流动模型不能兼容这些特征。

平衡流模式可用于估计覆盖地球表面几个纬度的气流中的风速。然而，在这种情况下，假设恒定的科里奥利参数是不现实的，可以局部应用平衡流速。将罗斯贝波作为纬度变化动态有效的示例。

不稳定

平衡流方法确定了从平衡气压模式得出的典型轨迹和稳态风速。实际上，气压模式和气团的运动是联系在一起的，因为气团在某处的积累（或密度增加）会增加地面气压，反之亦然。任何新的气压梯度都会导致新的空气置换，从而导致连续的重新排列。正如天气本身所表明的那样，稳态条件是例外的。

由于摩擦力、气压梯度和科里奥利力不一定平衡，气团实际上会加速和减速，因此实际速度也取决于其过去的值。如下所示，平衡流中气压场和流动轨迹的整齐排列，无论是平行还是成直角，都是基于稳定流动的假设。

稳态平衡流方程首先没有解释流动是如何运动的。此外，如果气压场变化得足够快，平衡流速无法帮助长距离跟踪气块，这仅仅是因为气块在移动时感受到的力发生了变化。与遵循原始气压场的情况相比，粒子将最终到达其他地方。

总之，平衡流方程给出了一致的稳态风速，可以估计特定时刻和特定地点的情况。从长远来看，这些速度不能可靠地用于了解空气向何处移动，因为强迫自然变化或轨迹相对于气压场是倾斜的。

逆流

逆流描述了在空间变化的气压场中的稳态流动，当

整个气压梯度完全平衡了摩擦力；
所有导致曲率的力都被忽略了。

这个名字来自希腊语“anti”（反对，反）和“triptein”（摩擦）——意思是这种流动通过反摩擦来进行。

公式

在流向动量方程中，摩擦力平衡了气压梯度分量而不是可忽略的（因此K ≠0）。气压梯度矢量仅由沿轨迹切线s的分量构成。

沿流向的平衡决定了逆向速度为 $V=-{\frac {1}{K\rho }}{\frac {\partial p}{\partial s}}$ 正速度是由逆流沿着气压场的向下斜率移动的事实保证的，因此在数学上 ${\partial p}/{\partial s}<0$ .假设乘积KV是恒定的且 ρ 保持不变，则p会随s线性变化，并且轨迹是这样的，即包裹在覆盖相等距离时感受到相等的压降。（当然，当使用非线性摩擦模型或在空间中变化的摩擦系数以允许不同的表面粗糙度时，这会发生变化。 )

在横流动量方程中，科里奥利力和法向气压梯度都可以忽略不计，导致没有净弯曲作用。作为离心项 ${V^{2}}/{R}$ 当速度不为零时消失，曲率半径趋于无穷大，轨迹必须是直线。此外，轨迹垂直于等压线，因为 $\partial p/\partial n=0$ .由于这种情况发生在n方向是等压线的方向时，所以s垂直于等压线。因此，反三等压线需要是等距的圆或直线。

应用

反三流可能是五种平衡流理想化中使用最少的，因为条件非常严格。然而，它是唯一一个下面的摩擦被认为是主要贡献的。因此，反三向模式适用于发生在地球表面附近的流动，即在称为恒定应力层的区域中。

实际上，恒定应力层中的流动也有一个平行于等压线的分量，因为它通常是由更快的流动驱动的。这是由于所谓的高报价下的自由空气流，往往平行于等压线，以及中间报价的埃克曼流，这导致自由空气速度降低和方向转向，同时接近表面。

由于科里奥利效应被忽略，反三向流动要么发生在赤道附近（与运动的长度尺度无关），要么除非流动的埃克曼数很大（通常用于小尺度过程）才能发生在其他地方，而不是出现地转流动。

反三向流可用于描述一些边界层现象，例如海风、埃克曼泵送和大平原的低空急流。 ^[1]

地转流

支持准地转条件的几乎平行的等压线

全球规模的西风气流大致沿平行线从拉布拉多（加拿大）穿过北大西洋，直至俄罗斯内陆

全球规模的东风西风流从俄罗斯横跨欧洲至中纬度大西洋，大致沿平行线跨越

一股偏北气流从北极流向北纬 40 度以南的中纬度地区

一股西北流位于两个大规模反向旋转的弯曲气流（旋风和反旋风）之间。关闭等压线表示高速

地转流描述了空间变化气压场中的稳态流动，当

摩擦效应被忽略；
整个气压梯度完全平衡了科里奥利力（导致没有曲率）。

这种情况称为地转平衡。 “geostrophic”这个名字源于希腊语“ge”（地球）和“strephein”（转动）。这种词源并不暗示轨迹的转向，而是绕地球旋转。

公式

在流向动量方程中，可忽略的摩擦由K = 0 表示，对于稳态平衡，可忽略的流向气压随之而来。

速度不能由这个平衡来决定。然而， $\partial p/\partial s=0$ 意味着轨迹必须沿着等压线运行，否则移动的包裹将经历气压变化，就像反三向流一样。因此，只有当等压线首先是直线时，才可能发生弯曲。因此，地转流表现为沿着这些等压线引导的流。

在横流动量方程中，不可忽略的科里奥利力由气压平衡，以使包裹不会受到任何弯曲作用。由于轨迹不弯曲，因此无法确定n的正方向，因为缺少曲率中心。在这种情况下，法线向量分量的符号变得不确定。然而，气压无论如何都必须完全抵消科里奥利力，因此空气团需要随着科里奥利力移动，这与气压的横向减小斜率相反。因此，不管形式上设置单位向量n的不确定性如何，包裹在北（南）半球的左（右）总是以较低的气压行进。

地转速度为 $V={\frac {1}{\rho }}\left|{\frac {1}{f}}{\frac {\partial p}{\partial n}}\right|.$ 地转速度的表达类似于反三向速度的表达：这里的速度由沿着（而不是穿过）等压线发展的轨迹上（而不是沿着）轨迹的气压梯度的大小决定。

应用

建模者、理论家和业务预报员经常使用地转/准地转近似。因为摩擦力不重要，地转平衡适合在地表上方足够高处的流动。因为科里奥利力是相关的，所以它通常适合具有较小罗斯贝数的过程，通常具有较大的长度尺度。与反三流条件相反，小埃克曼数的流动也实现了地转条件。

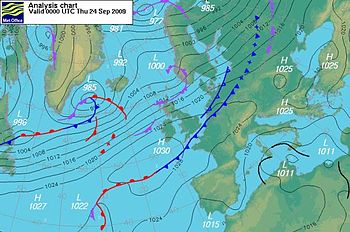
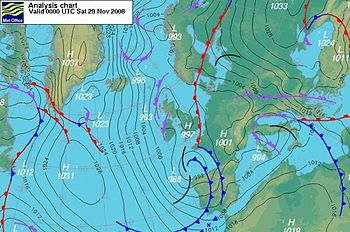
地转条件经常在明确的高压和低压对之间发展；或者主要的地转流两侧有几个高压和低压区域（见图）。尽管平衡流动方程不允许内部（空气对空气）摩擦，但地转流和附近旋转系统中的流动方向也与它们之间的剪切接触一致。

地转流的速度大于（小于）在具有相同气压梯度的低压（高压）周围的弯曲流中的速度：这个特征可以通过更一般的梯度流模式化来解释。这有助于将地转速度用作更复杂布置的粗略估计。

显示的术语和气压图表明地转流可以描述相当大尺度的大气运动，尽管实际情况不一定如此。

旋衡流

旋衡流（cyclostrophic flow）描述了在空间变化的气压场中的稳态流动，当

忽略摩擦和科里奥利作用；
向心加速度完全由气压梯度维持。

轨迹确实弯曲。 “cyclostrophic”这个名字源于希腊语“kyklos”（圆圈）和“strephein”（转身）。

公式

与地转平衡一样，流动是无摩擦的，对于稳态运动，轨迹遵循等压线。

在横流动量方程中，只去掉了科里奥利力，所以向心加速度就是单位质量的横流气压 ${\frac {V^{2}}{R}}=-{\frac {1}{\rho }}{\frac {\partial p}{\partial n}}.$ 这意味着轨迹受到弯曲作用，并且旋衡速度为 $V={\sqrt {-{\frac {R}{\rho }}{\frac {\partial p}{\partial n}}}}.$ 因此，旋衡速度由轨迹上气压梯度的大小和等压线的曲率半径决定。流动速度更快，离曲率中心越远，尽管不是线性的。

交叉流动量方程的另一个含义是旋衡流只能在低压区域旁边发展。这隐含在平方根下的数量为正的要求中。回想一下，旋衡轨迹被发现是等压线。只有当气压从曲率中心向外增加时，气压导数是负的并且平方根是明确定义的——因此曲率中心的气压必须很低。上面的数学没有给出旋转最终是顺时针还是逆时针的线索，这意味着最终的排列是关系中不允许的效应的结果，即父单元的旋转。

应用

当科里奥利力和摩擦力都可以忽略不计时，即对于具有大罗斯贝数和小埃克曼数的流动，旋衡流是现实的。科里奥利效应在低纬度或更小尺度上通常可以忽略不计。在诸如龙卷风、沙尘暴和水龙卷等系统中可以实现旋转平衡。回旋速度也可以看作是梯度平衡速度的贡献之一，如下所示。

在使用旋衡风模式化的研究中，Rennó 和 Bluestein ^[2]使用旋衡速度方程来构建水龙卷理论；和 Winn、Hunyady 和 Aulich ^[3]使用旋衡风近似计算 1995 年 6 月 8 日在德克萨斯州艾利森附近经过的大型龙卷风的最大切向风。

惯性流

惯性流（inertial flow）与所有其他流动不同，惯性平衡意味着均匀的气压场。在这个理想化模型中：

流动是无摩擦的；
不存在气压梯度（和力）。

剩下的力就是科里奥利力，它使得轨迹产生曲率。

公式

如前所述，稳态条件下的无摩擦流动意味着 $\partial p/\partial s=0$ .但是，在这种情况下，等压线首先没有定义。我们无法从气压场的排列中得出任何关于轨迹的预期。

在横流动量方程中，省略气压后，向心加速度为单位质量的科里奥利力。符号歧义消失了，因为弯曲完全由科里奥利力决定，该力使弯曲的一侧不受挑战 - 所以这个力总是一个正号。惯性旋转将在北（南）半球顺时针（逆时针）。动量方程：

${\frac {V^{2}}{R}}=\left|f\right|V,$ 可以推出惯性速度 $V=\left|f\right|R.$ 一旦给出了另一个，惯性速度方程仅有助于确定速度或曲率半径。这种运动产生的轨迹也称为惯性圆。平衡流模型没有给出惯性圆的初始速度的任何线索，它需要由一些外部扰动触发。

应用

由于大气运动主要是由气压差引起的，惯性流在大气动力学中不是很适用。然而，惯性速度似乎对梯度速度的解有贡献（见下文）。此外，在洋流中观察到惯性流动，由于密度较高，与空气相比，流动受气压差的驱动较少——惯性平衡可以在海洋较深处发生，使得由表面风向下传递的摩擦力基本可以忽略。

梯度流

梯度流（gradient flow）是地转流的延伸，因为它也考虑了曲率，使其更准确地近似于高层大气中的流动。然而，数学上梯度流稍微复杂一些，地转流可能相当准确，所以梯度近似并不经常被提及。

梯度流也是旋衡流的延伸，因为它允许科里奥利力的影响，使其适用于任何罗斯贝数的流动。最后，它还是惯性平衡的延伸，因为它允许气压梯度力来驱动流动。

公式

与除反三向平衡外的所有平衡一样，在流向动量方程中忽略了摩擦力和气压，因此它遵循 $\partial p/\partial s=0$ 流动平行于等压线。

将完整的交叉流动量方程求解为V的二次方程，得到 $V=\pm {\frac {fR}{2}}\pm {\sqrt {{\frac {f^{2}R^{2}}{4}}-{\frac {R}{\rho }}{\frac {\partial p}{\partial n}}}}.$ 并非所有梯度风速的解都会产生物理上合理的结果：由于速度的定义，右侧作为一个整体需要为正；并且平方根下的数量必须是非负的。第一个符号歧义来自科里奥利力和单位向量n的相互方向，而第二个来自平方根。

接下来讨论气旋和反气旋环流的重要情况。

低压和气旋

对于常规气旋（气压低点周围的空气循环），气压是向内的（正项），科里奥利力是向外的（负项），与半球无关。交叉轨迹动量方程为 ${\frac {V^{2}}{R}}={\frac {1}{\rho }}\left|{\frac {\partial p}{\partial n}}\right|-\left|f\right|V.$ 两边除以| f | V ，可发现： ${\frac {V_{\text{geostrophic}}}{V_{\text{cyclone}}}}=1+{\frac {V_{\text{cyclone}}}{V_{\text{inertial}}}}>1,$ 其中气旋梯度速度V小于相应的地转速度，不太准确的估计，并且随着曲率半径的增长（随着惯性速度趋于无穷大）自然地接近它。因此，在旋风分离器中，与地转速度的无曲率值相比，曲率会减慢流动速度。气旋方程的正根是 $V_{\text{cyclone}}=-{\frac {V_{\text{inertial}}}{2}}+{\sqrt {{\frac {V_{\text{inertial}}^{2}}{4}}+V_{\text{cyclostrophic}}^{2}}}.$ 显然根号内的项总是非负的值。

高压和反气旋

在反气旋（气压高点周围的空气循环）中，无论半球如何，科里奥利力总是向内（和正），而气压总是向外（和负）。交叉轨迹动量方程为 ${\frac {V^{2}}{R}}=-{\frac {1}{\rho }}\left|{\frac {\partial p}{\partial n}}\right|+\left|f\right|V.$ 两边除以| f | V ，我们得到 ${\frac {V_{\text{geostrophic}}}{V_{\text{anticyclone}}}}=1-{\frac {V_{\text{anticyclone}}}{V_{\text{inertial}}}}<1,$ 从而反气旋梯度速度V大于地转值并随着曲率半径变大而接近它。因此，在反气旋中，与（地转）无曲率值相比，等压线的曲率会加速气流。

V 有两个正根，但唯一符合地转条件限制的一个是 $V_{\text{anticyclone}}={\frac {V_{\text{inertial}}}{2}}-{\sqrt {{\frac {V_{\text{inertial}}^{2}}{4}}-V_{\text{cyclostrophic}}^{2}}}$ 这就要求 $V_{\text{inertial}}\geq 2V_{\text{cyclostrophic}}$ 。这个条件可以转化为这样的要求：给定一个在一定纬度上具有恒定气压斜率的高压区，在高压区周围一定有一个没有风的圆形区域。在其圆周上，空气以相应惯性速度的一半（以旋衡速度）运动，半径为 $R^{*}={\frac {4}{\rho f^{2}}}\left|{\frac {\partial p}{\partial n}}\right|,$ 通过解决R的上述不等式获得。在这个圆之外，随着曲率半径的增加，速度降低到地转值。这个半径的宽度随着气压梯度的强度而增长。

应用

梯度流可用于研究围绕具有小罗斯贝数的高压和低压中心旋转的大气流动。这是围绕气压中心的流动曲率半径较小的情况，并且地转流动不再以有用的准确度应用。

梯度风情形下的表面气压图

平衡流流速比较

在相同条件下，每个平衡流理想化都会对风速给出不同的估计。在这里，我们主要关注在高层大气中有效的模式。

首先，假设有一块空气样本在海面以上 500 米处流动，因此摩擦效应已经可以忽略不计。平均海平面以上 500 米处（干燥）空气的密度为 1.167 kg/m ³根据其状态方程。

其次，让驱动流动的气压用变化率来衡量，取为 1hPa/100公里（平均值）。回想一下，重要的不是气压的值，而是它在轨迹上变化的斜率。该斜率同样适用于直线等压线（地转流）或弯曲等压线（旋衡和梯度流）的间距。

第三，让包裹在 45 度的纬度上移动，无论是在南半球还是北半球——所以科里奥利力在使用 0.000115 赫兹的科里奥利参数时起作用。

平衡流速也随着轨迹/等压线的曲率半径 R 而变化。在圆形等压线的情况下，如示意图旋风分离器和反旋风分离器，曲率半径也是分别与低压和高压的距离。

取其中两个这样的距离 R ： 100公里和 300km，速度为（m/s）

	地转	旋衡	惯性	梯度（H-气压）	梯度（L-气压）
R=100 公里	7.45	9.25	11.50	不适用	5.15
R=300 公里	7.45	16.00	34.50	10.90	6.30

该图表显示了在上面选择的条件下以及随着曲率半径的增加，不同的速度如何变化。

地转速度（粉红色线）完全不依赖于曲率，它表现为一条水平线。然而，随着曲率半径变得无限大，气旋和反气旋的梯度速度接近它——地转平衡确实是梯度流动的极限情况，用于消失的向心加速度（即气压和科里奥利力完全平衡）。

旋衡速度（黑线）从零开始增加，其与 R 的增长率小于线性。实际上，无限的速度增长是不可能的，因为支持流动的条件在一定距离处发生了变化。还记得旋衡条件适用于小规模过程，因此外推到更高的半径在物理上没有意义。

与我们选择的气压梯度无关的惯性速度（绿线）从零开始线性增加，并且很快变得比其他任何速度都大得多。

梯度速度带有两条曲线，适用于低气压（蓝色）和高气压（红色）附近的速度。随着半径的增加，气旋环流中的风速从零开始增长，并且始终小于地转估计值。

在反气旋循环的例子中，260km 的距离内没有风（点 R*）——这是高压周围无风/低风的区域。在该距离处，第一个反气旋风的速度与旋衡风相同（Q 点），是惯性风（P 点）速度的一半。离点 R* 越远，反气旋风就越慢，并以越来越大的速度接近地转值。

曲线中还有另一个值得注意的点，标记为 S，其中惯性、旋衡和地转速度相等。 S 处的半径始终是 R* 的四分之一，即 65 公里处。

图解的一些限制也变得明显。例如，随着曲率半径沿子午线增加，纬度的相应变化意味着科里奥利参数的不同值，进而意味着力。相反，如果半径沿平行线，科里奥利力保持不变。所以，在循环流动的情况下，包裹的速度不太可能围绕整圈不及时变化，因为空气包裹在穿越不同纬度时会感受到不同强度的科里奥利力。此外，气压场很少采用整齐的圆形等压线形状，在整个圆圈周围保持相同的间距。此外，重要的密度差异也出现在水平平面中，例如当较暖的空气加入气旋环流时，从而在冷锋和暖锋之间形成了一个暖区。

另见

二次流

参考资料

^ Schaefer Etling, J.; C. Doswell. The Theory and Practical Application of Antitriptic Balance. Monthly Weather Review. 1980, 108 (6): 746–756. Bibcode:1980MWRv..108..746S. ISSN 1520-0493. doi:10.1175/1520-0493(1980)108<0746:TTAPAO>2.0.CO;2 .
^ Rennó, N.O.D.; H.B. Bluestein. A Simple Theory for Waterspouts. Journal of the Atmospheric Sciences. 2001, 58 (8): 927–932. Bibcode:2001JAtS...58..927R. ISSN 1520-0469. doi:10.1175/1520-0469(2001)058<0927:ASTFW>2.0.CO;2.
^ Winn, W.P.; S.J. Hunyady G.D. Aulich. Pressure at the ground in a large tornado. Journal of Geophysical Research. 1999, 104 (D18): 22,067–22,082. Bibcode:1999JGR...10422067W. doi:10.1029/1999JD900387 .

[1] Schaefer Etling, J.; C. Doswell. The Theory and Practical Application of Antitriptic Balance. Monthly Weather Review. 1980, 108 (6): 746–756. Bibcode:1980MWRv..108..746S. ISSN 1520-0493. doi:10.1175/1520-0493(1980)108<0746:TTAPAO>2.0.CO;2 .

[2] Rennó, N.O.D.; H.B. Bluestein. A Simple Theory for Waterspouts. Journal of the Atmospheric Sciences. 2001, 58 (8): 927–932. Bibcode:2001JAtS...58..927R. ISSN 1520-0469. doi:10.1175/1520-0469(2001)058<0927:ASTFW>2.0.CO;2.

[3] Winn, W.P.; S.J. Hunyady G.D. Aulich. Pressure at the ground in a large tornado. Journal of Geophysical Research. 1999, 104 (D18): 22,067–22,082. Bibcode:1999JGR...10422067W. doi:10.1029/1999JD900387 .

[1]

[2]

[3]