皮特里多邊形
在幾何學中,皮特里多邊形(Petrie polygon)是一種可以透過n維正多胞形的稜建構的扭歪多邊形,通常可以由n-1或以上(不含n)個維面上各取一稜構成。正多邊形的皮特里多邊形是其自身;而正多面體的皮特里多邊形是扭歪多邊形,因此正多面體的皮特里多邊形連續兩個邊都會位於同一個面[1][2]:161。皮特里多邊形一詞以約翰·弗林德斯·皮特里命名。
每個正多胞形都會存在一個正交投影,該正交投影能使對應幾何結構中其中一個皮特里多邊形被投影成正多邊形。這個被投影成正多邊形的皮特里多邊形會正好位於這個正交投影的最外圈,而其餘皮特里多邊形會呈現於其內部。而該扭歪多邊形所在的投影平面是對應幾何體之對稱性的考克斯特平面,而扭歪多邊形的邊數則是該考克斯特平面對應之考克斯特群的考克斯特數。這些多邊形和投影圖可用於可視化高維正圖形的對稱結構。
嵌入圖可以更廣義地定義皮特里多邊形。皮特里多邊形可以定義為同一個圖,嵌入在不同曲面時的面,而這種結構又稱為皮特里對偶。[3]
歷史
[编辑]約翰·弗林德斯·皮特里(John Flinders Petrie)是英國埃及學家弗林德斯·皮特里的獨生子。他生於1907年,自幼展現出了非凡的數學能力。全盛時期時的數學實力在高維幾何學上有出色的表現,他可以透過視覺化的方式來回答關於複雜四維物體的問題。他首先指出了在正多面體和高維正多胞形對應曲面上的扭歪正多邊形之重要性。考克斯特在1937年解釋了他和皮特里如何開始擴展正多面體經典主題的方式:[4]:33-62
- 在1926年的某天,約翰·弗林德斯·皮特里興奮地告訴我,他發現了兩個新的正多面體。他具有無窮多個面且沒有無效頂點。當我開始有點放下疑心時,他進一步地解釋道:其中一個正多面體由正方形組成,且每個頂點都是六個正方形的公共頂點[註 1]、而另一個正多面體由正六邊形組成,且每個頂點四個正六邊形的公共頂點[註 2][4]:33-62[註 3]。
1938年,皮特里與考克斯特找了派屈克·杜·瓦爾和H·T·弗拉等人合作研究並撰寫了書籍《五十九種二十面體》並出版[6]。考克斯特意識到皮特里使用的扭歪多邊形的幾何功能後,在他寫關於正多胞形的書籍時便以皮特里來命名此類多邊形。
皮特里多邊形的概念最初是定義於正多胞形上的,在後續的幾篇相關研究上,這個概念被推廣到半正多胞形上。[7]
正多面體的皮特里多邊形
[编辑]正多面體{p,q}和其對偶多面體{q,p}的皮特里多邊形包含在同一個正交投影中[7]。
| 扭歪四邊形 | 扭歪六邊形 | 扭歪十邊形 | ||
|---|---|---|---|---|

|

|

|
|

|

|

|

|

|

|
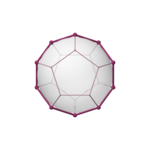
| 正四面體 {3,3} | 立方體 {4,3} | 正八面體 {3,4} | 正十二面體 {5,3} | 正二十面體 {3,5} |
| 稜為中心 | 角為中心 | 面為中心 | 面為中心 | 角為中心 |
| V:(4,0) | V:(6,2) | V:(6,0) | V:(10,10,0) | V:(10,2) |
|
皮特里多邊形是這些正交投影圖的周界。 | ||||
註解
[编辑]- ^ 即四角六片四角孔扭歪無限面體[4][5]。
- ^ 即六角四片四角孔扭歪無限面體[4][5]。
- ^ 原文為:One day in 1926, J. F. Petrie told me with much excitement that he had discovered two new regular polyhedral; infinite but free of false vertices. When my incredulity had begun to subside, he described them to me: one consisting of squares, six at each vertex, and one consisting of hexagons, four at each vertex.
參考文獻
[编辑]- ^ H. S. M. Coxeter. Discrete groups generated by reflections. Annals of Mathematics, Second Series. Jul., 1934,. Vol. 35 (No. 3): pp. 588-621.
- ^ F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss. Kaleidoscopes: Selected Writings of H. S. M. Coxeter. Wiley-Interscience Publication. 1995. ISBN 978-0-471-01003-6.
- ^ Gorini, Catherine A., Geometry at Work, MAA Notes 53, Cambridge University Press: 181, 2000, ISBN 9780883851647
- ^ 4.0 4.1 4.2 4.3 Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proceedings of the London Mathematical Society. (2) 43, 1937.
- ^ 5.0 5.1 いくろ こたろ. ねじれ多面体. geocities.jp. [2018-09-02]. (原始内容存档于2018-10-08).
- ^ H. S. M. Coxeter, Patrick du Val, H.T. Flather, J.F. Petrie (1938) The Fifty-nine Icosahedra, University of Toronto studies, mathematical series 6: 1–26
- ^ 7.0 7.1 Deza, Michel. Note on Petri duals and hypercube embeddings of semiregular polyhedra. Symmetry. 2011-01, 22.
- ^ Steinberg, Robert. On the number of sides of a Petrie polygon (PDF). Canadian Journal of Mathematics (Cambridge University Press). 1958, 10: 220–221.[失效連結]
