根系 (数学)

在數學中，根系是歐幾里得空間中滿足某些公理的向量配置。根系在李群、李代數與代數群理論中格外重要；而根系分類的主要工具──鄧肯圖，也見諸奇异性理论等與李群並無顯著關係的學科。

定義

設 $V$ 為有限維實向量空間，並賦予標準的內積 $(,)$ 。 $V$ 中的根系是有限個向量（稱為根）構成的集合 $\Phi$ ，滿足下述條件：

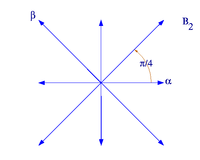
<α, β> 的整性條件使得 β 必然落在所示各條垂直線上。再配合 <β, α> 的整性條件，在每條線上，其間交角只有兩種可能。

$\Phi$ 的元素張出 $V$ 。
對任一 $\alpha \in \Phi$ ，其屬於 $\Phi$ 的純量倍數只有 $\pm \alpha$ 。
對任意 $\alpha \in \Phi$ ，集合 $\Phi$ 在對 $\alpha$ 的反射之下不變。在此的反射是指
$\sigma _{\alpha }(\beta )=\beta -2{\frac {(\alpha ,\beta )}{(\alpha ,\alpha )}}\alpha \in \Phi .$
（整性）若 $\alpha ,\beta \in \Phi$ ，則 $\beta$ 在 $\alpha$ 方向的投影乘以2是 $\alpha$ 的整數倍，即：
$\langle \beta ,\alpha \rangle :=2{\frac {(\alpha ,\beta )}{(\alpha ,\alpha )}}\in \mathbb {Z} ,$

根據性質三，整性等價於：對任意 $\alpha ,\beta \in \Phi$ ， $\sigma _{\alpha }(\beta )$ 與 $\beta$ 僅差 $\alpha$ 的整數倍。此外，注意到性質四定義的尖積

\langle \cdot ,\cdot \rangle \colon \Phi \times \Phi \to \mathbb {Z}

並非一個內積，它未必對稱，而且只對第一個參數是線性的。

根系 $\Phi$ 的秩定義為 $V$ 的維度。

給定兩個根系 $(V,\Phi ),(W,\Psi )$ ，可考慮其正交直和 $V\oplus W$ ，則 $\Phi \sqcup \Psi$ 自然地構成其中的根系。若一個根系無法表成如此的組合（當然，假設 $V,W\neq \{0\}$ ），則稱之為不可約的。

對兩個根系 $(E_{1},\Phi _{1}),(E_{2},\Phi _{2})$ ，若存在其間的線性同構，使得 $\Phi _{1}$ 映至 $\Phi _{2}$ ，則稱它們為同構的根系。

對於根系 $(V,\Phi )$ ，對根的反射生成一個群，稱為該根系的外爾群。可證明此群在 $\Phi$ 上忠實地作用，因此必為有限群。

秩一與秩二的例子

秩为1的例子

在同構的意義下，秩一的根系僅有一種，由兩個非零向量 $\{\alpha ,-\alpha \}$ 組成。此根系記作 $A_{1}$ 。

秩为2的例子

秩二的根系有四種可能，对应于 $\sigma _{\alpha }(\beta )=\beta +n\alpha$ ，其中 $n=0,1,2,3$ 的情况^[1]。注意根系并不由它生成的格所决定： $A_{1}\times A_{1}$ 和 $B_{2}$ 均生成正方形格，而 $A_{2}$ 和 $G_{2}$ 生成六边形格。这仅仅是五种可能的二维格中的两种。圖解如下：

**秩二之根系**

根系 A₁×A₁	根系 A₂

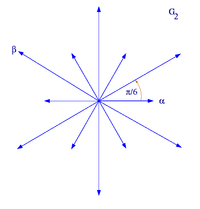
根系 B₂	根系 G₂

當 $\Phi$ 是 $V$ 中的根系，而 $W$ 是 $\Psi =\Phi \cap W$ 在 $W$ 中生成的子空間，則 $\Psi$ 是 $W$ 中的根系。因此上述列表限制了任意秩根系中兩根的幾何關係，例如：任意兩根的交角僅可能是 $0,30,45,60,90,120,135,150$ 或 $180$ 度。

正根與單根

對於根系 $\Phi$ ，可以取定滿足下述條件的正根子集 $\Phi ^{+}$ ：

對每個根 $\alpha \in \Phi$ ， $\alpha ,-\alpha$ 中恰有一者屬於 $\Phi ^{+}$ 。
對任意 $\alpha ,\beta \in \Phi ^{+}$ ，若 $\alpha +\beta \in \Phi$ ，則 $\alpha +\beta \in \Phi ^{+}$ 。

正根的取法並不唯一。取定一組正根後， $-\Phi ^{+}$ 的元素被稱為負根。

正根的選取等價於單根的選取。單根集是 $\Phi$ 中滿足下述條件的子集 $\Delta$ ：

任意

\Phi

中的元素皆可唯一地表成

\Delta

中元素的整係數線性組合，而且其係數或者全大於等於零，或者全小於等於零。

選定一組單根後，可定義相應的正根為展開式中係數大於等於零的根。如此可得到單根與正根選取法的一一對應。

以鄧肯圖分類根系

不可約根系與某類被稱為鄧肯圖的圖間有一一對應關係。鄧肯圖的分類是簡單的組合學問題，由此可導出不可約根系的分類定理。其構造方式如下：

給定一個不可約根系，選取一組單根。相應的鄧肯圖以這些單根為頂點。兩個單根 $\alpha ,\beta$ 若不垂直，則有 $\langle \alpha ,\beta \rangle \cdot \langle \beta ,\alpha \rangle$ 個邊相連：若只有一個邊，則不取定向，否則則取自長度 $(\alpha ,\alpha )$ 長者（稱為長根）指向短者（稱為短根）的有向邊。

一個根系可以取多種不同的單根。然而，由於外爾群在這些選取上的作用是傳遞的，鄧肯圖的構造與單根的選取無關，它是根系內在的不變量。反之，給定具有相同鄧肯圖的兩個不可約根系，可以按圖配對單根及其間的內積，從而得到根系的同構。鄧肯圖給出的內積未必唯一，但至多差一個正常數倍，因而得到的根系是同構的。

藉此，可將不可約根系的分類問題化約到連通鄧肯圖的分類。若某個鄧肯圖來自於根系，則從其頂點與邊定義的雙線性形式必然是鄧肯的；配上這個條件後，即可解決根系的分類。

鄧肯圖的分類列表詳如下圖。下標表示圖中的頂點數，亦即相應根系的秩。

不可約根系的性質

$\Phi$	$\|\Phi \|$	$\|\Phi ^{<}\|$	I	$\|W\|$
A_n (n≥1)	n(n+1)		n+1	(n+1)!
B_n (n≥2)	2n²	2n	2	2ⁿ n!
C_n (n≥3)	2n²	2n(n−1)	2	2ⁿ n!
D_n (n≥4)	2n(n−1)		4	2ⁿ⁻¹ n!
E₆	72		3	51840
E₇	126		2	2903040
E₈	240		1	696729600
F₄	48	24	1	1152
G₂	12	6	1	12

不可約根系依其鄧肯圖的種類命名。有四族根系： $A_{n},B_{n},C_{n},D_{n}$ ，其下標分別取遍 $n\geq 1,2,3,4$ 的正整數，稱為典型根系；剩下五種情形稱為例外根系。下標表示根系之秩。在上表中， $|\Phi ^{<}|$ 表示短根的個數（若諸根同長，則皆視為長根）， $I$ 表示其嘉當矩陣的行列式，而 $|W|$ 表示外爾群之階。

不可約根系的構造方法及描述

A_n

取 $V$ 為 $\mathbb {R} ^{n+1}$ 中滿足 $\sum _{i=1}^{n+1}x_{i}=0$ 的點 $(x_{1},\ldots ,x_{n+1})$ 所成之子空間。令 $\Phi$ 為 $V$ 中長度為 ${\sqrt {2}}$ 的格子點。取 $\mathbb {R} ^{n+1}$ 的標準基 $e_{1},\ldots ,e_{n+1}$ ，則根具有 $e_{i}-e_{j}\;(i\neq j)$ 的形式，共有 $n(n+1)$ 個根。通常取單根為 $\alpha _{i}:=e_{i}-e_{i+1}$ 。

對垂直於 $\alpha _{i}$ 的超平面的鏡射在 $\Phi$ 上的作用是交換第 $i,i+1$ 個座標。因此 $A_{n}$ 的外爾群不外就是對稱群 $S_{n+1}$ 。

$A_{n}$ 是李代數 ${\mathfrak {sl}}(n+1,\mathbb {C} )$ 的根系。

B_n

B₄
1	-1	0	0
0	1	-1	0
0	0	1	-1
0	0	0	1

取 $V=\mathbb {R} ^{n}$ ，並令 $\Phi$ 為 $V$ 中長度為 $1,{\sqrt {2}}$ 的格子點。共有 $2n^{2}$ 個根。通常取單根為 $\alpha _{i}=e_{i}-e_{i+1}\;(1\leq i<n)$ 及 $\alpha _{n}:=e_{n}$ （短根）。

對短根 $\alpha _{n}$ 的反射即 $(x_{1},\ldots ,x_{n})\mapsto (x_{1},\ldots ,-x_{n})$ 。

$B_{1}$ 跟 $A_{1}$ 僅差一個縮放，因此通常僅考慮 $n\geq 2$ 的情形。 $B_{n}$ 是李代數 ${\mathfrak {so}}(2n+1,\mathbb {C} )$ 的根系。

C_n

C₄
1	-1	0	0
0	1	-1	0
0	0	1	-1
0	0	0	2

取 $V=\mathbb {R} ^{n}$ ， $\Phi$ 為 $V$ 中所有長度 ${\sqrt {2}}$ 的格子點與形如 $2\lambda$ 的點，其中 $\lambda$ 是長度為一的格子點。共有 $2n^{2}$ 個根。通常取單根為 $\alpha _{i}:=e_{i}-e_{i+1}\;(1\leq i<n)$ 及 $\alpha _{n}:=2e_{n}$ （長根）。

$C_{2}$ 與 $B_{2}$ 僅差一個縮放加上旋轉 45 度，因此通常僅考慮 $n\geq 3$ 的情形。 $C_{n}$ 是李代數 ${\mathfrak {sp}}(2n,\mathbb {C} )$ 的根系。

D_n

D₄
1	-1	0	0
0	1	-1	0
0	0	1	-1
0	0	1	1

取 $V:=\mathbb {R} ^{n}$ ， $\Phi$ 為 $V$ 中長度 ${\sqrt {2}}$ 的格子點。共有 $2n(n-1)$ 個根。通常取單根為 $\alpha _{i}=e_{i}-e_{i+1},\;(1\leq i<n)$ 及 $\alpha _{n}=e_{n}+e_{n-1}$ 。

$D_{3}$ 同構於 $A_{3}$ ，故通常僅考慮 $n\geq 4$ 的情形。 $D_{n}$ 是李代數 ${\mathfrak {so}}(2n,\mathbb {C} )$ 的根系。

E₈, E₇, E₆

$E_{8}$ 是較為特殊的根系。首先定義 $\mathbb {R} ^{8}$ 中滿足下述條件的點集 $\Gamma _{8}$ ：

各座標均為整數，或均為半整數（不容相混）。
八個座標的和為偶數。

定義 $E_{8}$ 為 $\Gamma _{8}$ 中長度為 ${\sqrt {2}}$ 的向量，即：

\left\{\alpha \in \mathbb {Z} ^{8}\sqcup \left(\mathbb {Z} +{\frac {1}{2}}\right)^{8}:|\alpha |^{2}=2,\;\sum \alpha _{i}\in 2\mathbb {Z} \right\}

定義 $E_{7}$ 為 $E_{8}$ 與超平面 $\{x:(x,\alpha )=0\}$ 之交，其中 $\alpha \in E_{8}$ 是任取的根。同樣步驟施於 $E_{7}$ ，得到更小的根系 $E_{6}$ 。根系 $E_{6},E_{7},E_{8}$ 分別有 72, 126 與 240 個根。若續行此化約步驟，則會得到典型根系 $D_{5},A_{4}$ 。

E₈：偶坐標
1	-1	0	0	0	0	0	0
0	1	-1	0	0	0	0	0
0	0	1	-1	0	0	0	0
0	0	0	1	-1	0	0	0
0	0	0	0	1	-1	0	0
0	0	0	0	0	1	-1	0
0	0	0	0	0	1	1	0
½	½	½	½	½	½	½	½

另一種等價的描述是取 $\Gamma '_{8}$ 為：

各坐標均為整數，而且其和為偶數；或
各坐標均為半整數，而且其和為奇數。

$\Gamma _{8}$ 與 $\Gamma '_{8}$ 同構。將任意偶數個座標乘以負一，便可在兩者間轉換。 $\Gamma _{8}$ 稱為 $E_{8}$ 的偶坐標系， $\Gamma '_{8}$ 稱為奇坐標系。

在偶坐標下，通常取單根為

\alpha _{i}:=e_{i}-e_{i+1}\quad (1\leq i\leq 6)

\alpha _{7}:=e_{7}+e_{6}

\alpha _{8}=\beta _{0}={\frac {\sum _{i=1}^{8}e_{i}}{2}}

E₈：奇坐標
1	-1	0	0	0	0	0	0
0	1	-1	0	0	0	0	0
0	0	1	-1	0	0	0	0
0	0	0	1	-1	0	0	0
0	0	0	0	1	-1	0	0
0	0	0	0	0	1	-1	0
0	0	0	0	0	0	1	-1
-½	-½	-½	-½	-½	½	½	½

在奇坐標下，通常取單根為

\alpha _{i}:=e_{i}-e_{i+1}\quad (1\leq i\leq 7)

\alpha _{8}:=\beta _{5}

，其中

\beta _{j}:={\frac {-\sum _{i=1}^{j}e_{i}+\sum _{i=j+1}^{8}e_{i}}{2}}

（在上述定義中，若改取 $\beta _{3}$ ，將得到同構的結果。若改取 $\beta _{1},\beta _{7},\beta _{2},\beta _{6}$ ，將得到 $A_{8}$ 或 $D_{8}$ 。至於 $\beta _{4}$ ，其坐標和為零，而 $\alpha _{1},\ldots ,\alpha _{7}$ 亦然，所以張出的向量空間維度不合所求。

刪去 $\alpha _{1}$ 可得到 $E_{7}$ 的一組單根；再刪去 $\alpha _{2}$ ，可得 $E_{6}$ 的單根。

由於對 $\alpha _{1}$ 垂直等價於前兩個坐標相等，而對 $\alpha _{1},\alpha _{2}$ 垂直等價於前三個座標相等，不難導出 $E_{7},E_{6}$ 的明確定義：

E₇ = (α ∈ Z⁷ ∪ (Z+½)⁷: ∑α_i² + α₁² = 2，∑α_i + α₁ ∈ 2Z),

E₆ = (α ∈ Z⁶ ∪ (Z+½)⁶: ∑α_i² + 2α₁² = 2，∑α_i + 2α₁ ∈ 2Z)

F₄

F₄
1	-1	0	0
0	1	-1	0
0	0	1	0
-½	-½	-½	-½

對於 $F_{4}$ ，取 $V=\mathbb {R} ^{4}$ ，並令 $\Phi$ 為滿足下述條件的向量：

$|\alpha |=1,{\sqrt {2}}$
$2\alpha$ 各坐標皆為奇數或皆為偶數。

此根系有 $48$ 個根。通常取單根為 $B_{3}$ 的單根再加上 $\alpha _{4}=-\left(\sum _{i=1}^{4}e_{i}\right)/2$ 。

G₂

G₂
1	-1	0
-1	2	-1

$G_{2}$ 有 12 個根，構成一個六邊形的頂點，詳如秩二的例子一節所示。通常取單根為

$\alpha _{1}$
$\beta :=\alpha _{2}-\alpha _{1}$

在此沿用了之前的符號： $\alpha _{i}:=e_{i}-e_{i+1},\;(i=1,2)$ 。

根系與李群、李代數

不可約根系的分類可用於研究下述對象：

單複李代數
單複李群
模掉中心後為單李群的單連通複李群
緊單李群

参考文献

引用

^ Hall 2015 Proposition 8.8

来源

Serre, J.-P., Jones, G. A., Complex Semisimple Lie Algebras (2001), Springer-Verlag, ISBN 3540678271
Serre, J.-P. Lie Algebras and Lie Groups (2005), Lecture Notes in Mathematics, no. 1500, Springer-Verlag, ISBN 3540550089 .
Dynkin, E. B. The structure of semi-simple algebras. (Russian) Uspehi Matem. Nauk (N.S.) 2, (1947). no. 4(20), 59–127.
Hall, Brian C., Lie groups, Lie algebras, and representations: An elementary introduction, Graduate Texts in Mathematics 222 2nd, Springer, 2015, ISBN 978-3319134666

參見

[1] Hall 2015 Proposition 8.8

[1]

定義