双四角锥柱

双四角锥柱

类别	约翰逊多面体 J14 - J15 - J16
对偶多面体	双四角锥台
识别
名称	双四角锥柱
参考索引	J15
鲍尔斯缩写	esquidpy
性质
面	12
边	20
顶点	10
欧拉特征数	F=12, E=20, V=10 （χ=2）
组成与布局
面的种类	8个三角形 4个正方形
顶点图	2个(34) 8个(32.42)
对称性
对称群	D4h, [4,2], (*422)
旋转对称群	D4, [4,2]+, (422)
图像
双四角锥台 （对偶多面体） （展开图）

双四角锥柱是指以四边形为基底的双角锥柱，其可以由四角柱在两端各连接一个底面大小相同的四角锥来构成。若双四角锥柱的基底为正方形，且侧面都是正多边形的话，则这个立体是一种全部由正多边形组成的立体，为92种约翰逊多面体中的其中一个，其索引为J₁₅。约翰逊多面体是凸多面体，面皆由正多边形组成但不属于均匀多面体，共有92种。这些立体最早在1966年由诺曼·约翰逊（Norman Johnson）命名并给予描述。

双四角锥柱因其形似铅笔又称为铅笔立方体（pencil cube）或12面铅笔立方体（12-faced pencil cube）

性质

双四角锥柱共由12个面、20条边和10个顶点组成，在其12个面中，有8个三角形面和4个正方形面。在其10个顶点中，有两种顶点，一种顶点为4个三角形的公共顶点，在顶点图中可以用[3⁴]来表示，这种顶点有2个、另外一种顶点为2个三角形和2个正方形的公共顶点，在顶点图中可以用[3²,4²]来表示，这种顶点有8个。

体积与表面积

若一个双四角锥柱边长为$L$，则其体积$V$与表面积$A$为：

$V=L^{3}\cdot \left(1+{\frac {\sqrt {2}}{3}}\right)\approx L^{3}\cdot 1.471404521$

$A=L^{2}\cdot \left(4+2{\sqrt {3}}\right)\approx L^{2}\cdot 7.464101615$

这样的双四角锥柱整体的高$H$为：

$H=L\cdot \left(1+{\sqrt {2}}\right)\approx L\cdot 2.414213562$

二面角

双四角锥柱共有3种二面角，分别为三角形和正方形的二面角、三角形和三方形的二面角以及正方形和正方形的二面角。其中正方形和正方形的二面角为直角，即90度角。

$\angle$正方形$,$正方形$\,=90^{\circ }$

而三角形和正方形的二面角为负根号三分之二的反余弦值，约为144.7356度：

$\angle$三角形$,$正方形$\,=\arccos \left(-{\sqrt {\frac {2}{3}}}\right)\approx 2.52611294\approx 144.735610^{\circ }$

三角形和三方形的二面角为负三分之一的反余弦值，约为109.471度：

$\angle$三角形$,$三方形$\,=\arccos \left(-{\frac {1}{3}}\right)\approx 1.9106332\approx 109.471221^{\circ }$

顶点座标

若一个双四角锥柱边长为单位长，且几何中心位于原点，则其顶点座标为：

$\left(\pm {\frac {1}{2}},\,\pm {\frac {1}{2}},\,\pm {\frac {1}{2}}\right)$

$\left(0,\,0,\,\pm {\frac {1+{\sqrt {2}}}{2}}\right)$

相关多面体

一种非正多边形面的双四角锥柱的特例是空间填充多面体。这种双四角锥柱的三角形面不是正三角形，三角形的边长比为$2:{\sqrt {3}}:{\sqrt {3}}$。

其可以被认为是立方体堆砌和菱形十二面体堆砌之间的过渡立体。其胞在下图中根据它们在空间中的方向被着色为白色、红色和蓝色。其四角锥帽具有的面是较短的等腰三角形面，其中6个四角锥帽会聚在一起形成一个立方体。这种堆砌体的对偶是由两种八面体（正八面体和三角反棱柱）组成的，由八面体叠加到截半的立方体堆砌的中的截半立方体中形成。两种堆砌体都具有$\left[\left[4,3,4\right]\right]$对称性。

双四角锥柱堆砌

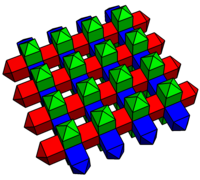一半的堆砌

倒角正方形镶嵌

双四角锥柱可以视为二侧锥的四角柱，也就是底面为四边形之柱体对应的二侧锥柱体，其他的二侧锥柱体有：

二侧锥柱体

侧锥方式	3	4	5	6	7	8
邻
	二侧锥三角柱	邻二侧锥四角柱	邻二侧锥五角柱	邻二侧锥六角柱	邻二侧锥七角柱	邻二侧锥八角柱
间	-	-
			间二侧锥五角柱	间二侧锥六角柱	间二侧锥七角柱	间二侧锥八角柱
对	-		-		-
		对二侧锥四角柱		对二侧锥六角柱		对二侧锥八角柱
1,4	-	-	-	-
					1,4-二侧锥七角柱	1,4-二侧锥八角柱

参见

• 约翰逊多面体
• 正多面体
• 正四角锥
• 正六面体