偏度

偏度不为零的实验数据样本（小麦胚芽鞘的向地反应：1,790）

偏度（英语：skewness），亦称歪度，在机率论和统计学中衡量实数随机变数概率分布的不对称性。偏度的值可以为正，可以为负或者甚至是无法定义。在数量上，偏度为负（负偏态；左偏）就意味着在概率密度函数左侧的尾部比右侧的长，绝大多数的值（不一定包括中位数在内）位于平均值的右侧。偏度为正（正偏态；右偏）就意味着在概率密度函数右侧的尾部比左侧的长，绝大多数的值（不一定包括中位数）位于平均值的左侧。偏度为零就表示数值相对均匀地分布在平均值的两侧，但不一定意味着其为对称分布。

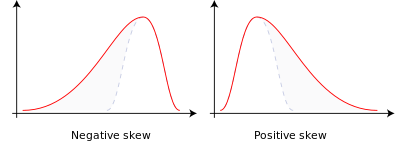负偏态（左）和正偏态（右）

介绍

偏度分为两种：

• 负偏态或左偏态：左侧的尾部更长，分布的主体集中在右侧。。
• 正偏态或右偏态：右侧的尾部更长，分布的主体集中在左侧。。

如果分布对称，那么平均值=中位数，偏度为零（此外，如果分布为单峰分布，那么平均值=中位数=众数）。

定义

随机变量$X$的偏度$\gamma _{1}$为三阶标准矩，可被定义为：

$\gamma _{1}=\operatorname {E} {\Big [}{\big (}{\tfrac {X-\mu }{\sigma }}{\big )}^{\!3}\,{\Big ]}={\frac {\mu _{3}}{\sigma ^{3}}}={\frac {\operatorname {E} {\big [}(X-\mu )^{3}{\big ]}}{\ \ \ (\operatorname {E} {\big [}(X-\mu )^{2}{\big ]})^{3/2}}}={\frac {\kappa _{3}}{\kappa _{2}^{3/2}}}\ ,$

其中$\mu _{3}$是三阶主动差，$\sigma$是标准差。$E$是期望算子。等式的最后以三阶累积量与二阶累积量的1.5次方的比率来表示偏度。这和用四阶累积量除去二阶累积量的平方来表示峰度的方法向类似。

偏度有时用$\mathrm {Skew} [X]$来表示。老教科书过去常常用${\sqrt {\beta _{1}}}$来表示偏度，可是由于偏度可为负，这样的表示法较为不便。

对上面的等式进行扩展可导出用非中心矩E[X³]来表示偏度的公式：

$\gamma _{1}=\operatorname {E} {\bigg [}{\Big (}{\frac {X-\mu }{\sigma }}{\Big )}^{\!3}\,{\bigg ]}={\frac {\operatorname {E} [X^{3}]-3\mu \operatorname {E} [X^{2}]+2\mu ^{3}}{\sigma ^{3}}}={\frac {\operatorname {E} [X^{3}]-3\mu \sigma ^{2}-\mu ^{3}}{\sigma ^{3}}}\ .$

样本偏度

具有$n$个值的样本的样本偏度为：

$g_{1}={\frac {m_{3}}{{m_{2}}^{3/2}}}={\frac {{\tfrac {1}{n}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{3}}{\left({\tfrac {1}{n}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}\right)^{3/2}}}\ ,$

其中${\overline {x}}$是样本平均值，$m_{3}$是三阶样本中心矩，$m_{2}$是二阶样本中心距，即样本方差。

性质

当： $\Pr \left[X>x\right]=x^{-3}{\mbox{ for }}x>1,\ \Pr[X<1]=0$ 时，偏度可以是无穷大的。

或者当： $\Pr[X<x]={\frac {(1-x)^{-3}}{2}}$（$x$为负）及

$\Pr[X>x]={\frac {(1+x)^{-3}}{2}}$（$x$为正）时，偏度无法定义。

在后面的这个例子中，三阶累积量是无法定义的。 其他分布形式比如：

$\Pr \left[X>x\right]=x^{-2}{\mbox{ for }}x>1,\ \Pr[X<1]=0$

二阶和三阶累积量是无穷大的，所以偏度也是无法定义的。

如果假定$Y$为$n$个独立变量之和并且这些变量和$X$具有相同的分布，那么$Y$的三阶累积量是$X$的$n$倍，$Y$的二阶累积量也是$X$的$n$倍，所以： ${\mbox{Skew}}[Y]={\frac {{\mbox{Skew}}[X]}{\sqrt {n}}}$。根据中心极限定理，当其接近高斯分布时变量之和的偏度减小。

参见

• 峰度
• 主动差

参考资料

• Groeneveld, RA; Meeden, G. Measuring Skewness and Kurtosis. The Statistician. 1984, 33 (4): 391–399 [2010-10-30]. doi:10.2307/2987742. （原始内容存档于2020-08-20）. 
• Johnson, NL, Kotz, S, Balakrishnan N (1994) Continuous Univariate Distributions, Vol 1, 2nd Edition Wiley ISBN 0-471-58495-9
• MacGillivray, HL. Shape properties of the g- and h- and Johnson families. Comm. Statistics - Theory and Methods. 1992, 21: 1244–1250.