实外代数中,
n 阶元素的几何诠释:
n = 0(具有正负号的点),1(具有指向的线段,即
向量),2(具有定向的平面元),3(具有定向的体积)。
n个向量的外积可以图像化为
n维几何物体(例如
n维
平行六面体,
n维
椭球);其大小为
超体积(hypervolume),其
定向的定义由
(n − 1)维边界以及物体内部在哪一侧来决定。
[1][2]外代数(英语:Exterior algebra)也称为格拉斯曼代数(Grassmann algebra),以纪念数学家赫尔曼·格拉斯曼。 本质是一个箭头,可进行的运算不多,不够灵活。而从对偶的角度,考虑切空间里的线性函数,则可以灵活的多,因为函数可以做加法、乘法、标量乘法、复合等运动[3]
数学上,向量空间 的外代数是一个特定有单位的结合代数,其包含了
的外代数是一个特定有单位的结合代数,其包含了 为其中一个子空间。它记为
为其中一个子空间。它记为 或
或 . 而它的乘法,称为楔积或外积,记为
. 而它的乘法,称为楔积或外积,记为 . 楔积是结合的和双线性的;其基本性质是它在
. 楔积是结合的和双线性的;其基本性质是它在 上是交错的,也就是:
上是交错的,也就是:
 ,对于所有向量
,对于所有向量
这表示
 ,对于所有向量
,对于所有向量 ,以及
,以及 ,当
,当 线性相关时。
线性相关时。
值得注意的是,以上三性质只对 中向量成立,不是对代数
中向量成立,不是对代数 中所有向量成立。
中所有向量成立。
外代数事实上是“最一般的”满足这些属性的代数。这意味着所有在外代数中成立的方程只从上述属性就可以得出。 的这个一般性形式上可以用一个特定的泛性质表示,请参看下文。
的这个一般性形式上可以用一个特定的泛性质表示,请参看下文。
形式为 的元素,其中
的元素,其中 在
在 中,称为
中,称为 -向量。所有
-向量。所有 -向量生成的
-向量生成的 的子空间称为
的子空间称为 的
的 -阶外幂,记为
-阶外幂,记为 。外代数可以写作每个
。外代数可以写作每个 阶幂的直和:
阶幂的直和:

该外积有一个重要性质,就是 -向量和
-向量和 -向量的积是一个
-向量的积是一个 -向量。这样外代数成为一个分次代数,其中分级由
-向量。这样外代数成为一个分次代数,其中分级由 给出。这些
给出。这些 -向量有几何上的解释:2-向量
-向量有几何上的解释:2-向量 代表以
代表以 和
和 为边的带方向的平行四边形,而3-向量
为边的带方向的平行四边形,而3-向量 代表带方向的平行六面体,其边为
代表带方向的平行六面体,其边为 ,
,  , 和
, 和 。
。
外幂的主要应用在于微分几何,其中他们用来定义微分形式。因而,微分形式有一个自然的楔积。所有这些概念由格拉斯曼提出。
外代数有很多种等价的定义,下面的定义是最简洁的一个。
定义: 设  是域
是域  上的一个向量空间,让
上的一个向量空间,让 则定义
则定义

令  为
为  的张量代数的理想(即双边理想),该理想是由所有形如
的张量代数的理想(即双边理想),该理想是由所有形如 的张量生成的(其中
的张量生成的(其中 任意),则将
任意),则将 上的外代数
上的外代数 定义为商代数
定义为商代数 ,即
,即

并且把 的等价类[4]
的等价类[4] ![{\displaystyle [v_{1}\otimes \ldots \otimes v_{k}]\in T(V)/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5148cc22666c1170f17014dfeffe7f75615447a4) 记为
记为 ,其中
,其中  。设
。设 称
称

为 的
的 -阶外幂(
-阶外幂( th exterior power of
th exterior power of  ),称
),称 中的元素为
中的元素为 -向量(
-向量( -multivector)。
-multivector)。
注:
 ,当且仅当
,当且仅当 时才有
时才有 ,因此,可以把
,因此,可以把 等同于
等同于 ,并且把
,并且把![{\displaystyle [\lambda ]\in \Lambda ^{0}(V)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87059ecf792985dc56378febbb4b00f6206e3f7b) 记为
记为 ;基于类似的原因,可以把
;基于类似的原因,可以把 等同于
等同于 ,而且把
,而且把![{\displaystyle [v]\in \Lambda ^{0}(V)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd9046713e2b3df3c380f0953dddd1217fc78741) 记为
记为 。这一点是前面所讲的能够把
。这一点是前面所讲的能够把![{\displaystyle [v_{1}\otimes \ldots \otimes v_{k}]\in \Lambda ^{k}(V)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22d259aecf2ba50066504b749521bef64542076b) 记为
记为  的特例和前提。
的特例和前提。- 当
 时,
时, -向量并不仅限于形如
-向量并不仅限于形如 的元素,例如,
的元素,例如, 也是2-向量,其中
也是2-向量,其中 .
.
- 理想
 中的元素并不仅限于形如
中的元素并不仅限于形如 的张量,例如,
的张量,例如,
 , 必定有
, 必定有  和
和 .
. , 由于
, 由于 和
和 以及
以及 ,显然有
,显然有 ,这就有一个推论:所有的二阶对称张量都在理想
,这就有一个推论:所有的二阶对称张量都在理想 中。
中。- 由于上面的两个结论,
 ,我们有
,我们有 ,这是因为等式右边的每一项都在
,这是因为等式右边的每一项都在 中。对张量
中。对张量 的阶数作数学归纳法,则可以证明:
的阶数作数学归纳法,则可以证明: ,
,  ,总有
,总有 。
。
- 设
 ,则
,则 ,
, 作为等价类含有唯一的一个完全反对称的代表元
作为等价类含有唯一的一个完全反对称的代表元 ,可以把这个
,可以把这个 -阶的完全反对称张量等同于
-阶的完全反对称张量等同于 , 详见后面的“反对称算子和外幂”一节。在有些文献中,
, 详见后面的“反对称算子和外幂”一节。在有些文献中, -向量就是以这种方式定义的。
-向量就是以这种方式定义的。
运算律 将上面的注中的内容用 写出,则分别给出
写出,则分别给出
(1)  ,
, 
证明如下: 作为等价类,我们从 中任意挑选一个代表元
中任意挑选一个代表元 ,则
,则 而且
而且![{\displaystyle \alpha =[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4be72fb8369a0b6808989320d3eba4c86f429909) 。根据商代数的定义,
。根据商代数的定义,
![{\displaystyle \lambda \wedge \alpha =[\lambda ]\wedge [t]=[\lambda \otimes t]=[\lambda t]=\lambda [t]=\lambda \alpha .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ede685179f9a4a99660bdcab23fc2cdb426b2599)
类似地,可以证明
(2) 根据注3.1中的内容,显然有 .
.
(3) 根据注3.2中的内容,对任意 成立着
成立着

注:即使 的特征为2,这个公式也是对的,只不过此时有
的特征为2,这个公式也是对的,只不过此时有 而已。
而已。
(4) 根据商代数的定义以及张量代数的性质,运算 满足结合律和分配律:
满足结合律和分配律:



其中 都是任意的。
都是任意的。
以前两条性质为例,其证明如下:设张量 分别是
分别是 中的代表元,即
中的代表元,即![{\displaystyle \alpha =[a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c56dee62ec8838b6cd786c13216890455a5d1d2) ,
, ![{\displaystyle \beta =[b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c935f2f60cd1e8d9d077d735f6d130ee5a74db1) ,
, ![{\displaystyle \theta =[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b0c8f339935b23b31c47564f326e8b93f9f9b8b) , 则
, 则
![{\displaystyle (\alpha \wedge \beta )\wedge \theta =([a]\wedge [b])\wedge [t]=[a\otimes b]\wedge [t]=[(a\otimes b)\otimes t]=[a\otimes (b\otimes t)]=[a]\wedge [b\otimes t]=[a]\wedge ([b]\wedge [t])=\alpha \wedge (\beta \wedge \theta ),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a92cda22d4dd50698f5df8052dddf5c3c1d9745)
![{\displaystyle (\alpha +\beta )\wedge \theta =([a]+[b])\wedge [t]=[a+b]\wedge [t]=[(a+b)\otimes t]=[a\otimes t+b\otimes t]=[a\otimes t]+[b\otimes t]=[a]\wedge [t]+[b]\wedge [t]=\alpha \wedge \theta +\beta \wedge \theta .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3731bec5812efe5762122dc15bdbca47fc40a1b4)
(5) 根据上面的(3)和(4),用数学归纳法可以证明:

证明从略。
若 的维数是
的维数是 而
而 是
是 的基,则集合
的基,则集合

是 阶外幂
阶外幂 的一个基。理由如下:给定任何如下形式的楔积
的一个基。理由如下:给定任何如下形式的楔积

则每个向量 可以记为基向量
可以记为基向量 的一个线性组合;利用楔积的双线性性质,这可以扩张为那些基向量的楔积的线性组合。任何出现同样基向量两次的楔积为0;任何基向量出现的次序不正确的可以重新排序,在交换任何两个基向量的时候变换符号。一般来讲,最后基
的一个线性组合;利用楔积的双线性性质,这可以扩张为那些基向量的楔积的线性组合。任何出现同样基向量两次的楔积为0;任何基向量出现的次序不正确的可以重新排序,在交换任何两个基向量的时候变换符号。一般来讲,最后基 -向量前的系数可以用通过积
-向量前的系数可以用通过积 来描述
来描述 的矩阵的子式来计算。
的矩阵的子式来计算。
数一下基元素,我们可以看到 的维数是n 取 k。特别的有,
的维数是n 取 k。特别的有,
 对于
对于 .
.
外代数是一个分级代数,是如下直和

其维数等于二项式系数之和,也就是 .
.
考虑空间 ,其基为
,其基为 。一对向量
。一对向量


的楔积为

其中 是三维空间
是三维空间 的基底。
的基底。
再加一个向量
 ,
,
这三个向量的楔积是

其中 是一维空间
是一维空间 的基底。
的基底。
空间 是
是 , 而空间
, 而空间 是
是 。取所有四个子空间的直和得到一个向量空间
。取所有四个子空间的直和得到一个向量空间 ,这是八维向量空间
,这是八维向量空间
 .
.
那么,给定一对8维向量 和
和 , 其中
, 其中 如上给出,而
如上给出,而
 ,
,
 和
和 的楔积如下(用列向量表达),
的楔积如下(用列向量表达),
 .
.
容易验证8维楔积以向量 为乘法幺元。也可以验证该
为乘法幺元。也可以验证该 代数的楔积是结合的(也是双线性的):
代数的楔积是结合的(也是双线性的):

所以该代数是有单位且结合的。
对三维欧几里得空间 可以建立一个线性同构
可以建立一个线性同构 如下:任取
如下:任取 的右手的标准正交基
的右手的标准正交基 ,
, ,
, ,规定
,规定 把
把 ,
, ,
, 分别映射为
分别映射为 ,
, ,
, ,则
,则 的定义与右手的标准正交基如何选取无关。
的定义与右手的标准正交基如何选取无关。
不难看出,对任意向量 和
和 ,这个线性同构把
,这个线性同构把 映射为
映射为 。这就是叉乘(向量积)的实质。例如,
。这就是叉乘(向量积)的实质。例如, 中平行四边形
中平行四边形 的面积向量可以表示为
的面积向量可以表示为 . 经过推广之后,高维黎曼流形
. 经过推广之后,高维黎曼流形 中的紧的二维曲面
中的紧的二维曲面 的面积则可以用
的面积则可以用

来计算(其中 是度规张量场
是度规张量场 在
在 上的诱导度规
上的诱导度规
 的坐标分量),由此可以看到外积和叉乘的深刻关系。
的坐标分量),由此可以看到外积和叉乘的深刻关系。
在物理学中,向量(极向量)与赝向量(轴向量)两个概念经常需要加以区分。从根本上说,向量是 中的元素,所以在空间反演变换下不会改变方向;而赝向量其实是
中的元素,所以在空间反演变换下不会改变方向;而赝向量其实是 中的元素,故在空间反演变换下会改变方向。
中的元素,故在空间反演变换下会改变方向。
类似地,借助于右手的标准正交基,可以把 中的元素
中的元素 映射为“标量"
映射为“标量" 。但是,在空间反演变换下它就会原形毕露,所以称它为赝标量。真正的标量在空间反演下是不变的,而赝标量在空间反演下会改变符号。
。但是,在空间反演变换下它就会原形毕露,所以称它为赝标量。真正的标量在空间反演下是不变的,而赝标量在空间反演下会改变符号。
把 2-向量 映射为向量
映射为向量 以及把 3-向量
以及把 3-向量 映射为一个实数
映射为一个实数 的映射实际上是一个叫做霍奇对偶的线性映射。
的映射实际上是一个叫做霍奇对偶的线性映射。
令 为一个域
为一个域 (在多数应用中,也就是实数域)上的向量空间。
(在多数应用中,也就是实数域)上的向量空间。 是“最一般”的包含
是“最一般”的包含 的并有一个交替乘法在
的并有一个交替乘法在 上由单位的结合
上由单位的结合 -代数这个事实可以用如下的泛性质形式化的表达:
-代数这个事实可以用如下的泛性质形式化的表达:
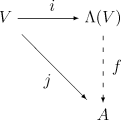 外代数的泛性质
外代数的泛性质
要构造最一般的包含 的代数,而且其乘法是在
的代数,而且其乘法是在 上交替的,很自然可以从包含
上交替的,很自然可以从包含 的最一般的代数开始,也就是张量代数
的最一般的代数开始,也就是张量代数 ,然后通过合适的商来强制交替的性质。这样我们取
,然后通过合适的商来强制交替的性质。这样我们取 中由所有形为
中由所有形为 的元素生成的双边理想
的元素生成的双边理想 ,其中
,其中 属于
属于 ,并定义
,并定义 为商
为商

(并且使用 为
为 中的乘法的代号)。然后可以直接证明
中的乘法的代号)。然后可以直接证明 包含
包含 并且满足上述泛性质。
并且满足上述泛性质。
如果不是先定义 然后把外幂
然后把外幂 等同为特定的子空间,我们也可以先定义空间
等同为特定的子空间,我们也可以先定义空间 然后把它们合并成为一个代数
然后把它们合并成为一个代数 。这个方法在微分集合中常常用到,并在下节中有描述。
。这个方法在微分集合中常常用到,并在下节中有描述。
给定两个向量空间 和
和 ,一个从
,一个从 到
到 的反对称算子是一个多线性映射
的反对称算子是一个多线性映射

使得只要 是
是 中线性相关的向量,则
中线性相关的向量,则
 .
.
最著名的例子是行列式值,从 到
到 的反对称线形算子。
的反对称线形算子。
映射

它关联 中的
中的 个向量到他们的楔积,也就是它们相应的
个向量到他们的楔积,也就是它们相应的 -向量,这也是反对称的。事实上,这个映射是定义在
-向量,这也是反对称的。事实上,这个映射是定义在 上的“最一般”的反对称算子:给定任何其它反对称算子
上的“最一般”的反对称算子:给定任何其它反对称算子 ,存在一个唯一的线性映射
,存在一个唯一的线性映射 。这个泛性质表述了空间
。这个泛性质表述了空间 并且可以作为它的定义。
并且可以作为它的定义。
所有从 到基域
到基域 的反对称映射组成一个向量空间,因为两个这样的映射的和、或者这样一个映射和一个标量的乘积也是反对称的。若
的反对称映射组成一个向量空间,因为两个这样的映射的和、或者这样一个映射和一个标量的乘积也是反对称的。若 是有限维的,维数
是有限维的,维数 ,则该空间可以认同为
,则该空间可以认同为 ,其中
,其中 表示
表示 的对偶空间。特别的有,从
的对偶空间。特别的有,从 到
到 的反对称映射的空间是
的反对称映射的空间是 取
取 维的。
维的。
在这个等同关系下,若基域是 或者
或者 ,楔积有一个具体的形式:它从两个给定的反对称映射得到一个新的反对称映射。设
,楔积有一个具体的形式:它从两个给定的反对称映射得到一个新的反对称映射。设 和
和 为两个反对称映射。和在多线性映射的张量积的情况一样,楔积的变量数是每个映射的变量数之和。它定义如下:
为两个反对称映射。和在多线性映射的张量积的情况一样,楔积的变量数是每个映射的变量数之和。它定义如下:

其中多线性映射的交替 定义为其变量的所有排列的带符号平均:
定义为其变量的所有排列的带符号平均:

注意: 有一些书中楔积定义为

在主要由物理学家使用的指标记法中有:

令 为一个微分流形。一个微分k-形式
为一个微分流形。一个微分k-形式 是
是 (
( 的余切丛的
的余切丛的 阶外幂)的一个截面。等价的有:
阶外幂)的一个截面。等价的有: 是
是 的光滑函数,对于
的光滑函数,对于 的每个点
的每个点 给定一个
给定一个 的元素。大致来讲,微分形式是余切向量的全局版本。微分形式是微分几何的重要工具,其中,它们被用于定义德拉姆上同调和亚历山大-斯潘尼尔上同调。
的元素。大致来讲,微分形式是余切向量的全局版本。微分形式是微分几何的重要工具,其中,它们被用于定义德拉姆上同调和亚历山大-斯潘尼尔上同调。
给定一个交换环 和一个
和一个 -模
-模 ,我们可以定义和上文一样的外代数
,我们可以定义和上文一样的外代数 ,它是张量代数
,它是张量代数 适当的商。它会满足类似的泛性质。
适当的商。它会满足类似的泛性质。
格拉斯曼代数在物理中有重要应用,它们被用于建模和费米子和超对称性相关的各种概念。
参看:超空间,超代数,超群
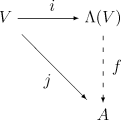

































![{\displaystyle [v_{1}\otimes \ldots \otimes v_{k}]\in T(V)/I}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5148cc22666c1170f17014dfeffe7f75615447a4)







![{\displaystyle [\lambda ]\in \Lambda ^{0}(V)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87059ecf792985dc56378febbb4b00f6206e3f7b)


![{\displaystyle [v]\in \Lambda ^{0}(V)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dd9046713e2b3df3c380f0953dddd1217fc78741)
![{\displaystyle [v_{1}\otimes \ldots \otimes v_{k}]\in \Lambda ^{k}(V)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22d259aecf2ba50066504b749521bef64542076b)

























![{\displaystyle \alpha =[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4be72fb8369a0b6808989320d3eba4c86f429909)
![{\displaystyle \lambda \wedge \alpha =[\lambda ]\wedge [t]=[\lambda \otimes t]=[\lambda t]=\lambda [t]=\lambda \alpha .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ede685179f9a4a99660bdcab23fc2cdb426b2599)












![{\displaystyle \alpha =[a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c56dee62ec8838b6cd786c13216890455a5d1d2)
![{\displaystyle \beta =[b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c935f2f60cd1e8d9d077d735f6d130ee5a74db1)
![{\displaystyle \theta =[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b0c8f339935b23b31c47564f326e8b93f9f9b8b)
![{\displaystyle (\alpha \wedge \beta )\wedge \theta =([a]\wedge [b])\wedge [t]=[a\otimes b]\wedge [t]=[(a\otimes b)\otimes t]=[a\otimes (b\otimes t)]=[a]\wedge [b\otimes t]=[a]\wedge ([b]\wedge [t])=\alpha \wedge (\beta \wedge \theta ),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a92cda22d4dd50698f5df8052dddf5c3c1d9745)
![{\displaystyle (\alpha +\beta )\wedge \theta =([a]+[b])\wedge [t]=[a+b]\wedge [t]=[(a+b)\otimes t]=[a\otimes t+b\otimes t]=[a\otimes t]+[b\otimes t]=[a]\wedge [t]+[b]\wedge [t]=\alpha \wedge \theta +\beta \wedge \theta .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3731bec5812efe5762122dc15bdbca47fc40a1b4)




























































































