一階保持(First-order hold、FOH)是一種重建信號的數學模型,可以透過傳統的數位類比轉換器(DAC)及稱為積分器的模擬電路完成。一階保持可以將訊號重建為分段線性近似原始訊號的函數。在實務上,像一階保持或零階保持之類的保持電路有其必要性。根據採樣定理,可以將離散後的訊號用狄拉克δ脈衝序列xs(t)表示,再經過低通濾波器即可還原到原始的訊號。不過實務上無法輸出狄拉克δ脈衝序列。利用傳統的數位類比轉換器以及一些線性類比電路就可以重建預測型或是延遲型的一階保持電路。
雖然在實務上的作法有所不同,但可以將假想的狄拉克δ脈衝序列xs(t)有特定特性的濾波器(若是線性時不變系統,可以用衝激響應完全描述其特性),因此每一個脈衝輸入都可以產生正確的分段線性輸出。
 理想取樣訊號xs(t).
理想取樣訊號xs(t).
一階保持是利用假想的濾波器或是線性時不變系統,將理想的取樣訊號

|

|
|
|

|
 分段連續信號xFOH(t).
分段連續信號xFOH(t).
轉換為分段線性的訊號。

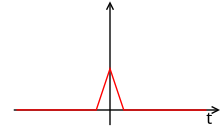 一階保持的衝激響應hFOH(t)(非因果)
一階保持的衝激響應hFOH(t)(非因果)
所得到的等效衝激響應為

- 其中
 是三角形函數
是三角形函數
等效頻率響應是衝激響應的傅里葉變換

|

|
|
|

|
|
|

|
- 其中
 是正規化的Sinc函數。
是正規化的Sinc函數。
可以令s = i 2 π f,得到FOH傳遞函數的拉普拉斯變換:

|

|
|
|

|
因為一階保持濾波器的衝激響應在t小於0時就已有值,因此此系統是反因果系統。
 有延遲的分段連續信號 xFOH(t).
有延遲的分段連續信號 xFOH(t).
延遲一階保持(Delayed first-order hold)有時也稱為因果一階保持(causal first-order hold)和一階保持相同,但輸出會延遲一個取樣週期才輸出,因此會有延遲的分段連續信號

 因果一階保持的衝激響應hFOH(t).
因果一階保持的衝激響應hFOH(t).
其等效衝激響應為

- 其中
 為三角形函數.
為三角形函數.
等效頻率響應是衝激響應的傅里葉變換

|

|
|
|

|
|
|

|
可以令s = i 2 π f,得到FOH傳遞函數的拉普拉斯變換:

|

|
|
|

|
延遲一階保持為因果系統。衝激響應在t小於0時沒有值。
這類的延遲一階保持可以用增益為H(z) = 1 − z−1的數字濾波器,將數字濾波器(x[n]−x[n−1])的輸出送到傳統的數位類比轉換器(本質上是零階保持),再用H(s) = 1/(sT)來積分DAC的輸出。
 預測型的分段連續信號xFOH(t).
預測型的分段連續信號xFOH(t).
預測型一階保持(predictive first-order hold)和上二一個一階保持的差異較大,預測型一階保持是因果系統的假想線性時不變系統,可以將理論取樣信號

|

|
|
|

|
轉換為分段線性輸出信號,會用目前取樣以及上一次的取様來線性外推下一個取樣點,此濾波器的輸出為

|

|
|
|

|
 預測型一階保持的衝激響應hFOH(t).
預測型一階保持的衝激響應hFOH(t).
其等效衝激響應為

|

|
|
|

|
- 其中
 為矩形函數,而
為矩形函數,而 為三角形函數。
為三角形函數。
等效頻率響應為衝激響應的傅里葉變換。

|

|
|
|

|
|
|

|
- 其中
 為Sinc函數。
為Sinc函數。
可以令s = i 2 π f,得到FOH傳遞函數的拉普拉斯變換]:

|

|
|
|

|
此為因果系統。預測型一階保持的衝激響應不會在輸入脈衝之前就出現。
這種分段線性的重建信號方式可以用增益H(z) = 1 − z−1</sup的數字濾波器來實現,將數位濾波器的輸出(就是x[n]−x[n−1])接到理想的傳統數位類比轉換器(其本質上是零階保持),將其輸出接到類比濾波器,其傳遞函數為H(s) = (1+sT)/(sT)。





































