六次方程

一個六次函數的圖像

六次方程是可以用下式表示的方程

$ax^{6}+bx^{5}+cx^{4}+dx^{3}+ex^{2}+fx+g=0$

其中a ≠ 0。 而六次函數是可以用下式表示的函數：

$f(x)=ax^{6}+bx^{5}+cx^{4}+dx^{3}+ex^{2}+fx+g$

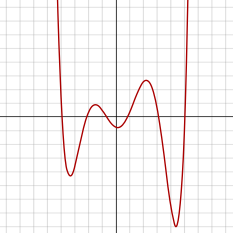
其中a ≠ 0。 六次函數也就是階數為6次的多項式，若a = 0，則多項式最多只為是五次函數。 若將令六次函數$y(x)=0$，即可得到六次方程。 六次方程的系數a, b, c, d, e, f, g可以是整數、有理數、複數或是任何一種體的元素。 因為六次函數的階數為偶數，其圖形類似二次函數及四次函數，不過會多兩個局部極值。其導函數為五次方程。

可以求解的六次方程

一部分六次方程可以通過因式分解求解，另一些無法求解。埃瓦里斯特·伽羅瓦發明了一種判斷一個六次方程是否可通過因式分解求解的方法，該方法後來發展成伽羅瓦理論。根據伽羅瓦理論，一個六次方程能用根式求解當且僅當它的伽羅瓦群包含於將根的集合劃分固定化（stabilize）成兩個根的三個子集的48階群或將根的集合劃分固定化（stabilize）成三個根的兩個子集的72階群。

存在公式可以測試這兩種情況，並在方程有解的時候求出用根式表示的根。

一般的六次方程可以通過Kampé de Fériet函數（超幾何函數的一個雙變量擴展版）求解。一類特殊的六次方程可以通過菲利克斯·克萊因求解五次方程的方法用超幾何函數的單變量一般化公式求出。

應用

蒸汽機早期設計中出現的瓦特曲線是一個二元六次方程。

求解三次方程時，有一種方法（叫韋達替換法，Vieta's substitution）是將該三次方程轉換成只有六次項、三次項和常數項的六次方程，再用二次方程解法將其解出。