慣性波

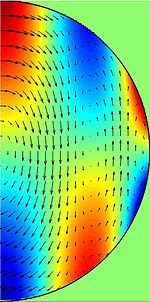
慣性波，也稱為慣性振盪、慣性內波，是一種可能出現在旋轉流體中的機械波。與通常在海灘或浴缸中看到的表面重力波不同，慣性波流過流體內部，而不是表面。與任何其他類型的波一樣，慣性波是由恢復力引起的，並以其波長和頻率為特徵。因為慣性波的恢復力是科里奧利力，它們的波長和頻率以一種特殊的方式相關。慣性波是橫向的。最常見的是在大氣、海洋、湖泊和實驗室實驗中觀察到它們。羅斯貝波、地轉流和地轉風是慣性波的例子。慣性波也可能存在於旋轉地球的熔融核心中。

恢復力

慣性波通過科里奧利力恢復平衡，這是旋轉的結果。準確地說，科里奧利力（與離心力一起）出現在旋轉框架中，以解釋這樣一個框架總是在加速的事實。因此，慣性波沒有旋轉就無法存在。科里奧利力比繩子上的張力更複雜，與運動方向成 90° 角，其強度取決於流體的旋轉速度。這兩個性質導致了慣性波的特殊特性。

特徵

慣性波只有在流體旋轉時才有可能，並且存在於流體的主體中，而不是在其表面。像光波一樣，慣性波是橫向的，這意味着它們的振動垂直於波的傳播方向發生。慣性波的一個獨特的幾何特徵是它們的相速度，它描述了波的波峰和波谷的運動，垂直於它們的群速度，它是能量傳播的量度。

儘管任何頻率的聲波或電磁波都是可能的，但慣性波只能存在於從零到流體旋轉速度兩倍的頻率範圍內。此外，波的頻率取決於其傳播方向。垂直於旋轉軸傳播的波的頻率為零，有時稱為地轉模式。平行於軸傳播的波具有最大頻率（旋轉速度的兩倍），中間角度的波具有中頻。在自由空間中，慣性波可以以介於 0 到兩倍旋轉速率之間的任何頻率存在。然而，一個封閉的容器可以對慣性波的可能頻率施加限制，就像對任何類型的波一樣。封閉容器中的慣性波通常稱為慣性模式。例如，在球體中，慣性模式被迫採用離散頻率，從而在不存在模式的地方留下間隙。

慣性波的例子

任何一種流體都可以支持慣性波：水、油、液態金屬、空氣和其他氣體。慣性波最常見於行星大氣（羅斯貝波、地轉風）以及海洋和湖泊（地轉流）中，它們負責大部分發生的混合。受海底坡度影響的慣性波通常稱為羅斯貝波。慣性波可以在實驗室實驗或流體旋轉的工業流中觀察到。慣性波也可能存在於地球的液態外核中，並且至少有一組[1] （頁面存檔備份，存於互聯網檔案館）聲稱存在它們的證據。同樣，慣性波也可能出現在旋轉的天文流中，如恆星、吸積盤、行星環和星系。

數學描述

流體流動由Navier-Stokes 動量方程控制。流速 ${\vec {u}}$ 具有粘性的流體 $\nu$ 在壓力之下 $P$ 並以速率旋轉 $\Omega$ 隨時間變化 $t$ 根據

{\frac {\partial {\vec {u}}}{\partial t}}+({\vec {u}}\cdot {\vec {\nabla }}){\vec {u}}=-{\frac {1}{\rho }}{\vec {\nabla }}P+\nu \nabla ^{2}{\vec {u}}-2{\vec {\Omega }}\times {\vec {u}}.

右側的第一項說明壓力，第二項說明粘性擴散，動量方程（上圖）右側的第三項（最後一項）是科里奧利項。

準確地說， ${\vec {u}}$ 是在旋轉參考系中觀察到的流速。由於旋轉參考系正在加速（即非慣性系），因此這種坐標變換會產生兩個附加（偽）力（如上所述）：離心力和科里奧利力。在上面的等式中，離心力作為廣義壓力 $P$ 的一部分，即 $P$ 與平時的壓力 $p$ 有關， $p$ 取決於與旋轉軸的距離 $r$ ，有下面的關係式：

P=p+{\frac {1}{2}}\rho r^{2}\Omega ^{2}.

在旋轉速度大的情況下，科里奧利力和離心力與其他項相比變大。相比之下，擴散和「對流導數」（左側第二項）可以忽略不計。取兩邊的旋度並應用一些向量恆等式，結果得：

{\frac {\partial }{\partial t}}\nabla \times {\vec {u}}=2({\vec {\Omega }}\cdot {\vec {\nabla }}){\vec {u}}.

該方程的一類解是滿足兩個條件的波。首先，如果 ${\vec {k}}$ 是波向量，

{\vec {u}}\cdot {\vec {k}}=0,

也就是說，波必須是橫向的，如上所述。第二，解需要頻率 $\omega$ 滿足色散關係

\omega =2{\hat {k}}\cdot {\vec {\Omega }}=2\Omega \cos {\theta },

其中 $\theta$ 是旋轉軸與波的方向之間的角度。這些特定的解被稱為慣性波。

色散關係看起來很像動量方程中的科里奧利項——注意旋轉速率和常係數2，它直接暗示了慣性波的可能頻率範圍，以及它們的頻率對其方向的依賴性。

延伸閱讀

Aldridge, K. D.; I. Lumb. Inertial waves identified in the Earth's fluid outer core. Nature. 1987, 325 (6103): 421–423. Bibcode:1987Natur.325..421A. S2CID 4312055. doi:10.1038/325421a0.
Greenspan, H. P. The Theory of Rotating Fluids. Cambridge University Press. 1969.
Landau, L. D.; E. M. Lifschitz. Fluid Mechanics, Second Edition. New York: Elsevier. 1987. ISBN 978-0-7506-2767-2.