图1:三维应力下的莫尔圆 莫尔圆 (Mohr's circle)得名自德国土木工程师克里斯汀·奥图·莫尔 柯西应力张量 转换关系的图。
先针对假设为连续 的物体进行应力分析 坐标系 有关。莫尔圆是用图形的方法去确认一个旋转坐标系上的应力分量,也就是在同一点上,但是作用在不同方向平面上的分量。
圆上每一个点的横坐标
σ
n
{\displaystyle \sigma _{\mathrm {n} }}
τ
n
{\displaystyle \tau _{\mathrm {n} }}
卡尔·卡尔曼 弯曲 时的纵向应力及垂直应力时所想到的。莫尔的贡献不止是用莫尔圆表示二维及三维的应力,他也根据莫尔圆发展了结构失效判定的准则[ 1]
其他表示应力状态的方式有拉梅应力椭球
莫尔圆可以扩展到对称 的 2x2 张量 ,包括应变 及转动惯量 张量。
图2:在有受力可变形物体(假设为连续体)中的应力F 考虑一个会变形的物体(假设为连续体),若受到外力(可能是表面力 或是物体力 欧拉运动定律 ,正如物体受力依循牛顿运动定律 一様。物体内部力的强度可以用应力 来表示。因为物体假设为连续体,其内部的力也是会均匀分布在其体积中。
在工程中(例如结构工程 、机械工程 或土力工程 )会透过应力分析 奥古斯丁·路易·柯西 的理论,(假设为连续体的)物体中任何一点的应力(图2),可以完全由二阶(2,0)型 张量 中的九个应力元素
σ
i
j
{\displaystyle \sigma _{ij}}
柯西应力张量 ,
σ
{\displaystyle {\boldsymbol {\sigma }}}
σ
=
[
σ
11
σ
12
σ
13
σ
21
σ
22
σ
23
σ
31
σ
32
σ
33
]
≡
[
σ
x
x
σ
x
y
σ
x
z
σ
y
x
σ
y
y
σ
y
z
σ
z
x
σ
z
y
σ
z
z
]
≡
[
σ
x
τ
x
y
τ
x
z
τ
y
x
σ
y
τ
y
z
τ
z
x
τ
z
y
σ
z
]
{\displaystyle {\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{x}&\tau _{xy}&\tau _{xz}\\\tau _{yx}&\sigma _{y}&\tau _{yz}\\\tau _{zx}&\tau _{zy}&\sigma _{z}\\\end{matrix}}\right]}
图3:连续体中的一点在平面应力条件下的应力转换 若确定了一物体在特定坐标系统
(
x
,
y
)
{\displaystyle (x,y)}
P
{\displaystyle P}
(
x
′
,
y
′
)
{\displaystyle (x',y')}
(
x
′
,
y
′
)
{\displaystyle (x',y')}
(
x
,
y
)
{\displaystyle (x,y)}
张量 的定义,柯西应力张量遵守张量转换定律。应力的莫尔圆是用图解方式来说明柯西应力张量转换定律的方式。
图4:连续体中的一点在平面应力条件下的应力分量 在二维下,一点
P
{\displaystyle P}
(
x
,
y
)
{\displaystyle (x,y)}
σ
x
{\displaystyle \sigma _{x}}
σ
y
{\displaystyle \sigma _{y}}
剪应力
τ
x
y
{\displaystyle \tau _{xy}}
τ
x
y
=
τ
y
x
{\displaystyle \tau _{xy}=\tau _{yx}}
σ
=
[
σ
x
τ
x
y
0
τ
x
y
σ
y
0
0
0
0
]
≡
[
σ
x
τ
x
y
τ
x
y
σ
y
]
{\displaystyle {\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{x}&\tau _{xy}&0\\\tau _{xy}&\sigma _{y}&0\\0&0&0\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{x}&\tau _{xy}\\\tau _{xy}&\sigma _{y}\\\end{matrix}}\right]}
其目的是在另一个通过
P
{\displaystyle P}
(
x
′
,
y
′
)
{\displaystyle (x',y')}
σ
n
{\displaystyle \sigma _{\mathrm {n} }}
τ
n
{\displaystyle \tau _{\mathrm {n} }}
(
x
′
,
y
′
)
{\displaystyle (x',y')}
(
x
,
y
)
{\displaystyle (x,y)}
θ
{\displaystyle \theta }
要推导二维平面应力 及平面应变的莫尔圆方程,先考虑一个位在位置
P
{\displaystyle P}
y
{\displaystyle y}
z
{\displaystyle z}
利用无限小元素上的力平衡,正向应力
σ
n
{\displaystyle \sigma _{\mathrm {n} }}
τ
n
{\displaystyle \tau _{\mathrm {n} }}
σ
n
=
1
2
(
σ
x
+
σ
y
)
+
1
2
(
σ
x
−
σ
y
)
cos
2
θ
+
τ
x
y
sin
2
θ
{\displaystyle \sigma _{\mathrm {n} }={\frac {1}{2}}(\sigma _{x}+\sigma _{y})+{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\cos 2\theta +\tau _{xy}\sin 2\theta }
τ
n
=
−
1
2
(
σ
x
−
σ
y
)
sin
2
θ
+
τ
x
y
cos
2
θ
{\displaystyle \tau _{\mathrm {n} }=-{\frac {1}{2}}(\sigma _{x}-\sigma _{y})\sin 2\theta +\tau _{xy}\cos 2\theta }
上述二个方程也可以用柯西应力张量的张量变换定律来求得,这和在
σ
n
{\displaystyle \sigma _{\mathrm {n} }}
τ
n
{\displaystyle \tau _{\mathrm {n} }}
这二个方程是莫尔圆的参数式 。在方程中,
2
θ
{\displaystyle 2\theta }
σ
n
{\displaystyle \sigma _{\mathrm {n} }}
τ
n
{\displaystyle \tau _{\mathrm {n} }}
σ
n
{\displaystyle \sigma _{\mathrm {n} }}
τ
n
{\displaystyle \tau _{\mathrm {n} }}
θ
{\displaystyle \theta }
若从参数式中消去参数
2
θ
{\displaystyle 2\theta }
σ
n
{\displaystyle \sigma _{\mathrm {n} }}
τ
n
{\displaystyle \tau _{\mathrm {n} }}
[
σ
n
−
1
2
(
σ
x
+
σ
y
)
]
2
+
τ
n
2
=
[
1
2
(
σ
x
−
σ
y
)
]
2
+
τ
x
y
2
(
σ
n
−
σ
a
v
g
)
2
+
τ
n
2
=
R
2
{\displaystyle {\begin{aligned}\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})\right]^{2}+\tau _{\mathrm {n} }^{2}&=\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}\\(\sigma _{\mathrm {n} }-\sigma _{\mathrm {avg} })^{2}+\tau _{\mathrm {n} }^{2}&=R^{2}\end{aligned}}}
其中
R
=
[
1
2
(
σ
x
−
σ
y
)
]
2
+
τ
x
y
2
and
σ
a
v
g
=
1
2
(
σ
x
+
σ
y
)
{\displaystyle R={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}\quad {\text{and}}\quad \sigma _{\mathrm {avg} }={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})}
这就是圆 (莫尔圆)的方程
(
x
−
a
)
2
+
(
y
−
b
)
2
=
r
2
{\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}}
在
(
σ
n
,
τ
n
)
{\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}
r
=
R
{\displaystyle r=R}
(
a
,
b
)
=
(
σ
a
v
g
,
0
)
{\displaystyle (a,b)=(\sigma _{\mathrm {avg} },0)}
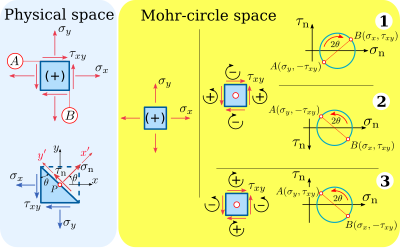
在使用莫尔圆时,需考虑两组分别的符号体系,一个是针对实体空间下应力分量的符号体系,另一个是针对“莫尔圆空间”下应力分量的符号体系。此外,工程力学(结构工程 及机械工程 )文献用的体系和地质力学
上述图4的莫尔圆推导都是使用工程力学的符号体系,以下也会继续使用工程力学的符号体系。
为了描述柯西应力张量的方便(图3及图4),应力分量的第一个下标表示应力分量作用的面,第二个下标表示应力分量的方向。因此
τ
x
y
{\displaystyle \tau _{xy}}
x
{\displaystyle x}
y
{\displaystyle y}
在实体空间符号体系,正的正向应力是由作用平面往外(张力),负的正向应力是由作用平面往内(压缩力)(图5)。
在实体空间符号体系中,正剪应力在法向量为正的材料元素平面上,其作用方向会往轴的正方向,同样的,正剪力在法向量为负的材料元素平面上,其作用方向会往轴的负方向。例如作用在正向平面的剪应力
τ
x
y
{\displaystyle \tau _{xy}}
τ
y
x
{\displaystyle \tau _{yx}}
y
{\displaystyle y}
x
{\displaystyle x}
τ
x
y
{\displaystyle \tau _{xy}}
τ
y
x
{\displaystyle \tau _{yx}}
y
{\displaystyle y}
x
{\displaystyle x}
图5 绘制莫尔圆时,工程力学符号体系下的应力。此条目会依照图中的符号体系 # 3 在莫尔圆空间符号体系中,应力的符号体系和实体空间符号体系中的相同:正的正向应力是由作用平面往外(张力),负的正向应力是由作用平面往内(压缩力)
不过剪应力的符号体系和实体空间符号体系中的不同。在莫尔圆空间符号体系中,正的剪应力会使材料往逆时针方向旋转,而负的剪应力会使材料往顺时针方向旋转。因此在莫尔圆空间中,剪应力分量
τ
x
y
{\displaystyle \tau _{xy}}
τ
y
x
{\displaystyle \tau _{yx}}
τ
x
y
{\displaystyle \tau _{xy}}
τ
y
x
{\displaystyle \tau _{yx}}
在绘制莫尔圆时,有二个作法可以绘制在数学上正确的莫尔圆:
将正的剪应力画在上方(图5,符号体系#1)
将正的剪应力画在下方,也就是
τ
n
{\displaystyle \tau _{\mathrm {n} }}
将正的剪应力画在上方会让莫尔圆上的
2
θ
{\displaystyle 2\theta }
[ 2]
2
θ
{\displaystyle 2\theta }
为了克服剪应力轴往下才是正向的问题,有另外一种“替代的”符号体系,其中正的剪应力假设为将材料将顺时针方向旋转,而负的剪应力假设为将材料将逆时针方向旋转(图5,符号体系#3)。在“替代”体系下,正的剪应力轴往上,而且在莫尔圆上
2
θ
{\displaystyle 2\theta }
τ
n
{\displaystyle \tau _{\mathrm {n} }}
τ
n
{\displaystyle \tau _{\mathrm {n} }}
此条目在实体空间符号体系中,会依照工程力学的符号体系,而在莫尔圆空间中,会使用“替代的”符号体系(图5,符号体系#3)。
图6:在平面应力及平面应变的条件下绘制莫尔圆(二倍角的作法)
P
{\displaystyle P}
σ
x
{\displaystyle \sigma _{x}}
σ
y
{\displaystyle \sigma _{y}}
τ
x
y
{\displaystyle \tau _{xy}}
A
{\displaystyle A}
B
{\displaystyle B}
P
{\displaystyle P}
A
{\displaystyle A}
B
{\displaystyle B}
A
{\displaystyle A}
B
{\displaystyle B}
σ
n
{\displaystyle \sigma _{\mathrm {n} }}
τ
n
{\displaystyle \tau _{\mathrm {n} }}
D
{\displaystyle D}
O
B
¯
{\displaystyle {\overline {OB}}}
O
D
¯
{\displaystyle {\overline {OD}}}
P
{\displaystyle P}
B
{\displaystyle B}
D
{\displaystyle D}
假设已知待研究物体上的点
P
{\displaystyle P}
σ
x
{\displaystyle \sigma _{x}}
σ
y
{\displaystyle \sigma _{y}}
τ
x
y
{\displaystyle \tau _{xy}}
P
{\displaystyle P}
绘制笛卡尔坐标系统
(
σ
n
,
τ
n
)
{\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}
σ
n
{\displaystyle \sigma _{\mathrm {n} }}
τ
n
{\displaystyle \tau _{\mathrm {n} }}
在
(
σ
n
,
τ
n
)
{\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}
A
(
σ
y
,
τ
x
y
)
{\displaystyle A(\sigma _{y},\tau _{xy})}
B
(
σ
x
,
−
τ
x
y
)
{\displaystyle B(\sigma _{x},-\tau _{xy})}
A
{\displaystyle A}
B
{\displaystyle B}
用线段
A
B
¯
{\displaystyle {\overline {AB}}}
A
{\displaystyle A}
B
{\displaystyle B}
绘制莫尔圆,其圆心
O
{\displaystyle O}
A
B
¯
{\displaystyle {\overline {AB}}}
σ
n
{\displaystyle \sigma _{\mathrm {n} }}
主要应力的大小是点
C
{\displaystyle C}
E
{\displaystyle E}
σ
n
{\displaystyle \sigma _{\mathrm {n} }}
σ
1
{\displaystyle \sigma _{1}}
σ
2
{\displaystyle \sigma _{2}}
σ
1
=
σ
max
=
σ
avg
+
R
{\displaystyle \sigma _{1}=\sigma _{\max }=\sigma _{\text{avg}}+R}
σ
2
=
σ
min
=
σ
avg
−
R
{\displaystyle \sigma _{2}=\sigma _{\min }=\sigma _{\text{avg}}-R}
其中平均正向应力
σ
avg
{\displaystyle \sigma _{\text{avg}}}
O
{\displaystyle O}
σ
avg
=
1
2
(
σ
x
+
σ
y
)
{\displaystyle \sigma _{\text{avg}}={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})}
其半径的长度
R
{\displaystyle R}
R
=
[
1
2
(
σ
x
−
σ
y
)
]
2
+
τ
x
y
2
{\displaystyle R={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}}
最大剪应力和最小剪应力对应圆上最大及最小的纵坐标。这二个点是圆和通过圆心
O
{\displaystyle O}
R
{\displaystyle R}
τ
max
,
min
=
±
R
{\displaystyle \tau _{\max ,\min }=\pm R}
如前面所述,在二维应力分析后,可以知道在材料某一点
P
{\displaystyle P}
σ
x
{\displaystyle \sigma _{x}}
σ
y
{\displaystyle \sigma _{y}}
τ
x
y
{\displaystyle \tau _{xy}}
P
{\displaystyle P}
A
{\displaystyle A}
B
{\displaystyle B}
D
{\displaystyle D}
σ
n
{\displaystyle \sigma _{\mathrm {n} }}
τ
n
{\displaystyle \tau _{\mathrm {n} }}
D
{\displaystyle D}
P
{\displaystyle P}
B
{\displaystyle B}
θ
{\displaystyle \theta }
如图6所示,若平面
D
{\displaystyle D}
B
{\displaystyle B}
θ
{\displaystyle \theta }
D
{\displaystyle D}
(
σ
n
,
τ
n
)
{\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}
B
(
σ
x
,
−
τ
x
y
)
{\displaystyle B(\sigma _{x},-\tau _{xy})}
2
θ
{\displaystyle 2\theta }
D
(
σ
n
,
τ
n
)
{\displaystyle D(\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}
O
B
¯
{\displaystyle {\overline {OB}}}
O
D
¯
{\displaystyle {\overline {OD}}}
2
θ
{\displaystyle 2\theta }
倍角法的作法源自于通过
P
{\displaystyle P}
θ
{\displaystyle \theta }
(
σ
n
,
τ
n
)
{\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}
倍角关系是因为莫尔圆的参数式是
2
θ
{\displaystyle 2\theta }
P
{\displaystyle P}
A
{\displaystyle A}
B
{\displaystyle B}
图7:平面应力及应变的莫尔圆(极点法)。从极点画的任何直线都会和莫尔圆相交,交点表示在和直线相同角度平面上的应力状态 第二种方式和要找到莫尔圆上的一个点,称为极点(pole)或是平面原点(origin of planes)。从极点画的任何直线都会和莫尔圆相交,交点表示在和直线相同角度的平面上的应力状态。因此若知道任何特定平面上的应力分量
σ
{\displaystyle \sigma }
τ
{\displaystyle \tau }
σ
n
{\displaystyle \sigma _{\mathrm {n} }}
τ
n
{\displaystyle \tau _{\mathrm {n} }}
σ
x
,
{\displaystyle \sigma _{x},\!}
σ
y
,
{\displaystyle \sigma _{y},\!}
τ
x
y
,
{\displaystyle \tau _{xy},\!}
B
{\displaystyle B}
σ
x
{\displaystyle \sigma _{x}}
A
{\displaystyle A}
σ
y
{\displaystyle \sigma _{y}}
θ
{\displaystyle \theta }
最大主要应力及最小主要应力所在的平面方向也称为主要平面(principal planes),可以用莫尔圆中
的∠BOC及∠BOE判断,然后将二个角度都取一半。因此
O
B
¯
{\displaystyle {\overline {OB}}}
O
C
¯
{\displaystyle {\overline {OC}}}
θ
p
{\displaystyle \theta _{p}}
B
{\displaystyle B}
而
θ
p
1
{\displaystyle \theta _{p1}}
θ
p
2
{\displaystyle \theta _{p2}}
tan
2
θ
p
=
2
τ
x
y
σ
x
−
σ
y
{\displaystyle \tan 2\theta _{\mathrm {p} }={\frac {2\tau _{xy}}{\sigma _{x}-\sigma _{y}}}}
此方程的解会是二个角度,彼此相差
90
∘
{\displaystyle 90^{\circ }}
τ
n
{\displaystyle \tau _{\mathrm {n} }}
图10 三维应力下的莫尔图 若要绘制三维应力下的莫尔图,需要先量测其主应力 的大小
(
σ
1
,
σ
2
,
σ
3
)
{\displaystyle \left(\sigma _{1},\sigma _{2},\sigma _{3}\right)}
(
n
1
,
n
2
,
n
3
)
{\displaystyle \left(n_{1},n_{2},n_{3}\right)}
考虑以主应力轴为坐标系统,而不是用
x
1
{\displaystyle x_{1}}
x
2
{\displaystyle x_{2}}
x
3
{\displaystyle x_{3}}
σ
1
>
σ
2
>
σ
3
{\displaystyle \sigma _{1}>\sigma _{2}>\sigma _{3}}
n
{\displaystyle \mathbf {n} }
T
(
n
)
{\displaystyle \mathbf {T} ^{(\mathbf {n} )}}
(
T
(
n
)
)
2
=
σ
i
j
σ
i
k
n
j
n
k
σ
n
2
+
τ
n
2
=
σ
1
2
n
1
2
+
σ
2
2
n
2
2
+
σ
3
2
n
3
2
{\displaystyle {\begin{aligned}\left(T^{(n)}\right)^{2}&=\sigma _{ij}\sigma _{ik}n_{j}n_{k}\\\sigma _{\mathrm {n} }^{2}+\tau _{\mathrm {n} }^{2}&=\sigma _{1}^{2}n_{1}^{2}+\sigma _{2}^{2}n_{2}^{2}+\sigma _{3}^{2}n_{3}^{2}\end{aligned}}}
σ
n
=
σ
1
n
1
2
+
σ
2
n
2
2
+
σ
3
n
3
2
.
{\displaystyle \sigma _{\mathrm {n} }=\sigma _{1}n_{1}^{2}+\sigma _{2}n_{2}^{2}+\sigma _{3}n_{3}^{2}.}
由于
n
i
n
i
=
n
1
2
+
n
2
2
+
n
3
2
=
1
{\displaystyle n_{i}n_{i}=n_{1}^{2}+n_{2}^{2}+n_{3}^{2}=1}
n
1
2
{\displaystyle n_{1}^{2}}
n
2
2
{\displaystyle n_{2}^{2}}
n
3
2
{\displaystyle n_{3}^{2}}
n
1
2
=
τ
n
2
+
(
σ
n
−
σ
2
)
(
σ
n
−
σ
3
)
(
σ
1
−
σ
2
)
(
σ
1
−
σ
3
)
≥
0
n
2
2
=
τ
n
2
+
(
σ
n
−
σ
3
)
(
σ
n
−
σ
1
)
(
σ
2
−
σ
3
)
(
σ
2
−
σ
1
)
≥
0
n
3
2
=
τ
n
2
+
(
σ
n
−
σ
1
)
(
σ
n
−
σ
2
)
(
σ
3
−
σ
1
)
(
σ
3
−
σ
2
)
≥
0.
{\displaystyle {\begin{aligned}n_{1}^{2}&={\frac {\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{2})(\sigma _{\mathrm {n} }-\sigma _{3})}{(\sigma _{1}-\sigma _{2})(\sigma _{1}-\sigma _{3})}}\geq 0\\n_{2}^{2}&={\frac {\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{3})(\sigma _{\mathrm {n} }-\sigma _{1})}{(\sigma _{2}-\sigma _{3})(\sigma _{2}-\sigma _{1})}}\geq 0\\n_{3}^{2}&={\frac {\tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{1})(\sigma _{\mathrm {n} }-\sigma _{2})}{(\sigma _{3}-\sigma _{1})(\sigma _{3}-\sigma _{2})}}\geq 0.\end{aligned}}}
因为
σ
1
>
σ
2
>
σ
3
{\displaystyle \sigma _{1}>\sigma _{2}>\sigma _{3}}
(
n
i
)
2
{\displaystyle (n_{i})^{2}}
τ
n
2
+
(
σ
n
−
σ
2
)
(
σ
n
−
σ
3
)
≥
0
{\displaystyle \tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{2})(\sigma _{\mathrm {n} }-\sigma _{3})\geq 0}
σ
1
−
σ
2
>
0
{\displaystyle \sigma _{1}-\sigma _{2}>0}
σ
1
−
σ
3
>
0
{\displaystyle \sigma _{1}-\sigma _{3}>0}
τ
n
2
+
(
σ
n
−
σ
3
)
(
σ
n
−
σ
1
)
≤
0
{\displaystyle \tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{3})(\sigma _{\mathrm {n} }-\sigma _{1})\leq 0}
σ
2
−
σ
3
>
0
{\displaystyle \sigma _{2}-\sigma _{3}>0}
σ
2
−
σ
1
<
0
{\displaystyle \sigma _{2}-\sigma _{1}<0}
τ
n
2
+
(
σ
n
−
σ
1
)
(
σ
n
−
σ
2
)
≥
0
{\displaystyle \tau _{\mathrm {n} }^{2}+(\sigma _{\mathrm {n} }-\sigma _{1})(\sigma _{\mathrm {n} }-\sigma _{2})\geq 0}
σ
3
−
σ
1
<
0
{\displaystyle \sigma _{3}-\sigma _{1}<0}
σ
3
−
σ
2
<
0.
{\displaystyle \sigma _{3}-\sigma _{2}<0.}
方程式可以写成
τ
n
2
+
[
σ
n
−
1
2
(
σ
2
+
σ
3
)
]
2
≥
(
1
2
(
σ
2
−
σ
3
)
)
2
τ
n
2
+
[
σ
n
−
1
2
(
σ
1
+
σ
3
)
]
2
≤
(
1
2
(
σ
1
−
σ
3
)
)
2
τ
n
2
+
[
σ
n
−
1
2
(
σ
1
+
σ
2
)
]
2
≥
(
1
2
(
σ
1
−
σ
2
)
)
2
{\displaystyle {\begin{aligned}\tau _{\mathrm {n} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{2}+\sigma _{3})\right]^{2}\geq \left({\tfrac {1}{2}}(\sigma _{2}-\sigma _{3})\right)^{2}\\\tau _{\mathrm {n} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{1}+\sigma _{3})\right]^{2}\leq \left({\tfrac {1}{2}}(\sigma _{1}-\sigma _{3})\right)^{2}\\\tau _{\mathrm {n} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{1}+\sigma _{2})\right]^{2}\geq \left({\tfrac {1}{2}}(\sigma _{1}-\sigma _{2})\right)^{2}\\\end{aligned}}}
是三个应力莫尔圆
C
1
{\displaystyle C_{1}}
C
2
{\displaystyle C_{2}}
C
3
{\displaystyle C_{3}}
R
1
=
1
2
(
σ
2
−
σ
3
)
{\displaystyle R_{1}={\tfrac {1}{2}}(\sigma _{2}-\sigma _{3})}
R
2
=
1
2
(
σ
1
−
σ
3
)
{\displaystyle R_{2}={\tfrac {1}{2}}(\sigma _{1}-\sigma _{3})}
R
3
=
1
2
(
σ
1
−
σ
2
)
{\displaystyle R_{3}={\tfrac {1}{2}}(\sigma _{1}-\sigma _{2})}
[
1
2
(
σ
2
+
σ
3
)
,
0
]
{\displaystyle \left[{\tfrac {1}{2}}(\sigma _{2}+\sigma _{3}),0\right]}
[
1
2
(
σ
1
+
σ
3
)
,
0
]
{\displaystyle \left[{\tfrac {1}{2}}(\sigma _{1}+\sigma _{3}),0\right]}
[
1
2
(
σ
1
+
σ
2
)
,
0
]
{\displaystyle \left[{\tfrac {1}{2}}(\sigma _{1}+\sigma _{2}),0\right]}
有了上述三个应力莫尔圆的方程,所有可能的应力点
(
σ
n
,
τ
n
)
{\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}
(
σ
n
,
τ
n
)
{\displaystyle (\sigma _{\mathrm {n} },\tau _{\mathrm {n} })}
C
1
{\displaystyle C_{1}}
C
1
{\displaystyle C_{1}}
C
2
{\displaystyle C_{2}}
C
2
{\displaystyle C_{2}}
C
3
{\displaystyle C_{3}}
C
3
{\displaystyle C_{3}}
Beer, Ferdinand Pierre; Elwood Russell Johnston; John T. DeWolf. Mechanics of Materials . McGraw-Hill Professional. 1992. ISBN 0-07-112939-1 Brady, B.H.G.; E.T. Brown. Rock Mechanics For Underground Mining Third. Kluwer Academic Publisher. 1993: 17–29 [2018-02-05 ] . ISBN 0-412-47550-2原始内容 存档于2020-08-07). Davis, R. O.; Selvadurai. A. P. S. Elasticity and geomechanics . Cambridge University Press. 1996: 16–26 [2018-02-05 ] . ISBN 0-521-49827-9原始内容 存档于2020-08-07). Holtz, Robert D.; Kovacs, William D. An introduction to geotechnical engineering . Prentice-Hall civil engineering and engineering mechanics series. Prentice-Hall. 1981 [2018-02-05 ] . ISBN 0-13-484394-0原始内容 存档于2019-06-08). Jaeger, John Conrad; Cook, N.G.W; Zimmerman, R.W. Fundamentals of rock mechanics Fourth. Wiley-Blackwell. 2007: 9–41 [2018-02-05 ] . ISBN 0-632-05759-9原始内容 存档于2019-06-02). Jumikis, Alfreds R. Theoretical soil mechanics: with practical applications to soil mechanics and foundation engineering . Van Nostrand Reinhold Co. 1969 [2018-02-05 ] . ISBN 0-442-04199-3原始内容 存档于2019-06-08). Parry, Richard Hawley Grey. Mohr circles, stress paths and geotechnics 2. Taylor & Francis. 2004: 1–30 [2018-02-05 ] . ISBN 0-415-27297-1原始内容 存档于2020-08-07). Timoshenko, Stephen P.; James Norman Goodier. Theory of Elasticity Third. McGraw-Hill International Editions. 1970. ISBN 0-07-085805-5 Timoshenko, Stephen P. History of strength of materials: with a brief account of the history of theory of elasticity and theory of structures . Dover Books on Physics. Dover Publications. 1983. ISBN 0-486-61187-6 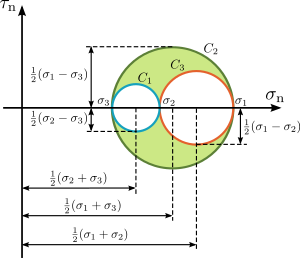











![{\displaystyle {\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{x}&\tau _{xy}&\tau _{xz}\\\tau _{yx}&\sigma _{y}&\tau _{yz}\\\tau _{zx}&\tau _{zy}&\sigma _{z}\\\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/150f0bb6d0473b0cc572e736e3f0c61ae490cf0e)







![{\displaystyle {\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{x}&\tau _{xy}&0\\\tau _{xy}&\sigma _{y}&0\\0&0&0\\\end{matrix}}\right]\equiv \left[{\begin{matrix}\sigma _{x}&\tau _{xy}\\\tau _{xy}&\sigma _{y}\\\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/946034030fac5e3d547e35f94ac672ed9dbc87d2)













![{\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}'&=\mathbf {A} {\boldsymbol {\sigma }}\mathbf {A} ^{T}\\\left[{\begin{matrix}\sigma _{x'}&\tau _{x'y'}\\\tau _{y'x'}&\sigma _{y'}\\\end{matrix}}\right]&=\left[{\begin{matrix}a_{x}&a_{xy}\\a_{yx}&a_{y}\\\end{matrix}}\right]\left[{\begin{matrix}\sigma _{x}&\tau _{xy}\\\tau _{yx}&\sigma _{y}\\\end{matrix}}\right]\left[{\begin{matrix}a_{x}&a_{yx}\\a_{xy}&a_{y}\\\end{matrix}}\right]\\&=\left[{\begin{matrix}\cos \theta &\sin \theta \\-\sin \theta &\cos \theta \\\end{matrix}}\right]\left[{\begin{matrix}\sigma _{x}&\tau _{xy}\\\tau _{yx}&\sigma _{y}\\\end{matrix}}\right]\left[{\begin{matrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{matrix}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c98aac6cba73c966e89d772397263f69ee507e4d)







![{\displaystyle {\begin{aligned}\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})\right]^{2}+\tau _{\mathrm {n} }^{2}&=\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}\\(\sigma _{\mathrm {n} }-\sigma _{\mathrm {avg} })^{2}+\tau _{\mathrm {n} }^{2}&=R^{2}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2774a663ddaa56d3418815d5a7d05fcf456d6f12)
![{\displaystyle R={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}\quad {\text{and}}\quad \sigma _{\mathrm {avg} }={\tfrac {1}{2}}(\sigma _{x}+\sigma _{y})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a7f5d5e3408c2d465f9e463c5576810f83d2401)
























![{\displaystyle R={\sqrt {\left[{\tfrac {1}{2}}(\sigma _{x}-\sigma _{y})\right]^{2}+\tau _{xy}^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb62b3753948e2c8cbcc4b054de4f34d9630d711)






































![{\displaystyle {\begin{aligned}\tau _{\mathrm {n} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{2}+\sigma _{3})\right]^{2}\geq \left({\tfrac {1}{2}}(\sigma _{2}-\sigma _{3})\right)^{2}\\\tau _{\mathrm {n} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{1}+\sigma _{3})\right]^{2}\leq \left({\tfrac {1}{2}}(\sigma _{1}-\sigma _{3})\right)^{2}\\\tau _{\mathrm {n} }^{2}+\left[\sigma _{\mathrm {n} }-{\tfrac {1}{2}}(\sigma _{1}+\sigma _{2})\right]^{2}\geq \left({\tfrac {1}{2}}(\sigma _{1}-\sigma _{2})\right)^{2}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d28046575eb3837044e07c9c8b3c6d70e641087b)






![{\displaystyle \left[{\tfrac {1}{2}}(\sigma _{2}+\sigma _{3}),0\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d32d3b2fb09d202625baa0df42fc08db094ce4c5)
![{\displaystyle \left[{\tfrac {1}{2}}(\sigma _{1}+\sigma _{3}),0\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be6108f95fb1e9bf64d2e770f8e220e91505d59b)
![{\displaystyle \left[{\tfrac {1}{2}}(\sigma _{1}+\sigma _{2}),0\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04758ef4c7e5169326291b5857f30c6ae9f83dee)