五维超正方体
| 五维超正方体 （10超胞体） | |
|---|---|
 | |
| 类型 | 五维凸正多胞体 |
| 家族 | 立方形 |
| 维度 | 5 |
| 对偶多胞形 | 五维正轴体 |
| 类比 | 正方体 |
| 识别 | |
| 鲍尔斯缩写 | pent |
| 数学表示法 | |
| 考克斯特符号 |      |
| 施莱夫利符号 | {4,3,3,3} {4,33} {4,3,3}×{} {4,3}×{4} {4,3}×{}×{} {4}×{4}×{} {4}×{}×{}×{} {}×{}×{}×{}×{} |
| 性质 | |
| 四维胞 | 10 {4,3,3}  |
| 胞 | 40（4.4.4） |
| 面 | 80 {4}  |
| 边 | 80 |
| 顶点 | 32 |
| 特殊面或截面 | |
| 皮特里多边形 | 十边形 |
| 组成与布局 | |
| 顶点图 |  正五胞体 |
| 对称性 | |
| 对称群 | BC5, [3,3,3,4] |
| 特性 | |
| 凸 | |
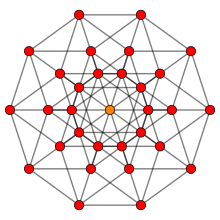
五维超立方体（Penteract）或称正十超胞体（Decateron）是3个五维凸正多超胞体之一，是五维的超方形，四维超正方体、三维正方体、二维正方形的五维类比。由10个四维超立方体胞、40个正方体胞、80个正方形面、80条棱、32个顶点组成。
几何性质
[编辑]五维超正方体存在于五维欧几里得空间中，其32个顶点有如下形式：
- （±1,±1,±1,±1,±1）
五维超正方体是它们的凸包。它包含了所有坐标值绝对值都小于等于1的所有点。在它的顶点处有5条棱相交，应此它的顶点图是正五胞体，在它的棱处有4个立方体维脊相交，应此它的棱图是正四面体。它有施莱夫利符号{4,3,3,3}，考斯特-迪肯符号，它的对偶多超胞体是正三十二超胞体（Triacontaditeron），也叫五维正轴体（Pentacross，5-orthoplex）。
对称群构造
[编辑]作为五维的立方形，一个五维凸正多超胞体，它具有BC5对称群构造，对应施莱夫利符号{4,3,3,3}，考斯特-迪肯符号。同时，它可被看作是四维超正方体的棱柱，对应施莱夫利符号{4,3,3}×{}，考斯特-迪肯符号。并且，它还是正方形和立方体的乘积，在3个维度有立方体的对称性BC3，而在另外两个维度表现出正方形的对称性BC2，施莱夫利符号{4,3}×{4}，考斯特-迪肯符号。
图像
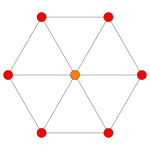
[编辑]五维超立方体可以以自身的BCn（n≤5）对称性被平行投影到2维平面上：
| 考克斯特平面 | B5 | B4 / D5 | B3 / D4 / A2 |
|---|---|---|---|
| 图像 |
|
|
|
| 二面体群 | [10] | [8] | [6] |
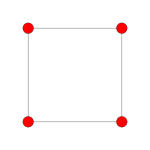
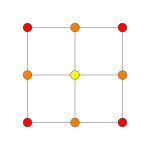
| 考克斯特平面 | 使棱在前 | B2 | A3 |
| 图像 | 
|
|
|
| 二面体群 | [2] | [4] | [4] |
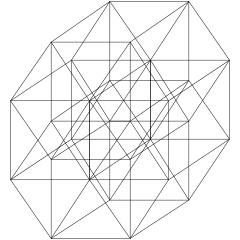 斜线架投影 |
 B5考克斯特平面 |
 顶点—棱图象。 |
 五维超立方体的5D到4D施莱尔投影的4D到3D球极投影的3D到2D透视投影 |
在五维空间旋转的透视投影 |
相关链接
[编辑]参考文献
[编辑]- H.S.M.考克斯特：
- Coxeter, Regular Polytopes,（3rd edition, 1973）, Dover edition, ISBN 0-486-61480-8, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions（n≥5）
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]（页面存档备份，存于互联网档案馆）
- （Paper 22）H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- （Paper 23）H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- （Paper 24）H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- 詹森·诺曼 Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.（1966）
- Klitzing, Richard. 5D uniform polytopes (polytera) o3o3o3o4x - pent. bendwavy.org.
- 埃里克·韦斯坦因. Hypercube. MathWorld.
- Olshevsky, George, Measure polytope at Glossary for Hyperspace.
- Multi-dimensional Glossary: hypercube（页面存档备份，存于互联网档案馆） Garrett Jones
| 五维正多胞体 | ||
|---|---|---|
| 五维正六胞体 | 五维超正方体 | 五维正三十二胞体 |
| {3,3,3,3} | {4,3,3,3} | {3,3,3,4} |
