匹配漸近展開法(英語:method of matched asymptotic expansions)是數學中用於獲得方程或方程組高精度近似解的一種常用方法,尤其常用於奇異攝動微分方程的求解。
對於許多奇異攝動問題而言,可以將定義域分成兩個或多個部分。其中一部分(通常是範圍最大的部分)可以通過正則攝動理論獲得漸近展開級數解。然而這個解在其他較小的部分則十分不精確。如果這些部分處於定義域邊界上被稱為邊界層,處於定義域中間則稱為內層。可以將邊界層或內層內的求解問題當作一個獨立的攝動問題處理,以獲得相應的「內解」(之前通過正則攝動獲得的則稱為「外解」)。最後再將內解與外解通過「匹配」的辦法合併,以得到在整個定義域內都適用的近似解。[1][2][3]
考慮邊值問題

其中 為時間
為時間 的函數,定義域從0到1,邊界條件為
的函數,定義域從0到1,邊界條件為 與
與 。
。 是一個小參數,滿足
是一個小參數,滿足 。
。
由 十分小,故可以當作正則攝動問題處理。取
十分小,故可以當作正則攝動問題處理。取 ,有
,有

該方程的解為

其中 為常數。使用邊界條件
為常數。使用邊界條件 ,有
,有 。而如果使用另一個邊界條件
。而如果使用另一個邊界條件 ,則有
,則有 。這說明該解不可能滿足所有邊界條件,意味著
。這說明該解不可能滿足所有邊界條件,意味著 的假設不能在整個定義域中都適用(即奇異攝動問題)。於是,我們能夠知道定義域中必定存在一個邊界層,其中
的假設不能在整個定義域中都適用(即奇異攝動問題)。於是,我們能夠知道定義域中必定存在一個邊界層,其中 與自變量
與自變量 相比不能再忽略不計。這個邊界層位於
相比不能再忽略不計。這個邊界層位於 一側。於是我們使用另一個邊界條件
一側。於是我們使用另一個邊界條件 得到適用於邊界層以外區域的外解
得到適用於邊界層以外區域的外解 。
。
在邊界層之內, 與
與 都很小,但它們大小相若,故可以定義一個新的O(1) 時間變量
都很小,但它們大小相若,故可以定義一個新的O(1) 時間變量 。於是原先的邊值問題可以改寫為
。於是原先的邊值問題可以改寫為

將兩邊同乘 再取
再取 ,得到
,得到

該方程的解為

其中 與
與 為常數。使用邊界層內的邊界條件
為常數。使用邊界層內的邊界條件 ,得到
,得到 。故內解為
。故內解為

由於對於中間大小的 (
( )需同時滿足內解和外解,故可以令內解的外極限與外解的內極限相等,即
)需同時滿足內解和外解,故可以令內解的外極限與外解的內極限相等,即 。由此得到常數
。由此得到常數 。
。
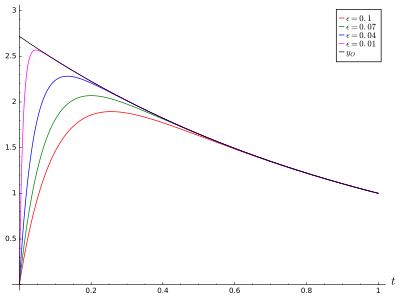
 取不同值時的近似解
取不同值時的近似解
最後,將匹配好的內解與外解合併,以得到適用於整個定義域的近似解。具體而言,即是將內解與外解相加,再減去內、外解重合部分的值 (即外解的內極限,或內解的外極限)。此問題中,重合部分的值為
(即外解的內極限,或內解的外極限)。此問題中,重合部分的值為 。故可以得到原邊值問題的最終近似解為
。故可以得到原邊值問題的最終近似解為































